🎨 CG | Bresenham 算法和三角形光栅化

Bresenham 算法在进行直线的扫描转换时，由于不涉及浮点数运算，只是整数类型的运算，所以大大提高了计算速率。由于 Bresenham 算法精简、高效的特性，当前已经完全由硬件实现。这里就来了解算法背后的原理，尝试自己用GL_POINTS绘制一些图案

🚀 代码: Github

绘制点

因为下面所有操作都是通过绘制点来操作的，因此可以将这个操作简单地封装起来

首先定义两个函数，addPoint负责把点添加到顶点对象中，drawPoint负责把点绘制出来

class Points: public Application {
public:
  void drawPoint();
  void addPoint();
  // ...
private:
  int canvas_size;
  int point_count;
  int vertices[1000000];
  float finalVertices[1000000];
  // ...
}

// 画点
void Points::addPoint(int x, int y) {
  vertices[point_count++] = x;
  vertices[point_count++] = y;
}

因为下面地所有操作都是整数运算的，而 OpenGL 默认渲染的坐标系是$[-1, 1]$的浮点数。因此还需要缩放一下坐标。

canvas_size定义了整个屏幕画布的大小，这里默认值为 100
point_count表示当前缓冲区的点的数量
vertices为当前整数顶点缓冲区
finalVertices为最终的输出顶点缓冲区

为了优化性能，每次我们把所有点都计算出来加入整数缓冲区，最后才调用drawPoint将整数缓冲区转换为最终的顶点缓冲区调用OpenGL的函数将所有的点绘制出来

void Points::drawPoint() {
  // 缩放为-1到1
  for (int j = 0; j < point_count; j++) {
    finalVertices[j] = vertices[j] * (1.0f / canvas_size);
  }
  // 顶点数组对象
  unsigned int VAO;
  glGenVertexArrays(1, &VAO);
  // 顶点缓冲对象
  unsigned int VBO;
  glGenBuffers(1, &VBO);
  // 绑定缓冲
  glBindVertexArray(VAO);
  glBindBuffer(GL_ARRAY_BUFFER, VBO);
  // 点的大小
  glPointSize(point_size);
  // 复制数据
  glBufferData(GL_ARRAY_BUFFER, sizeof(finalVertices), finalVertices, GL_STATIC_DRAW);
  // 解析顶点数据
  glVertexAttribPointer(0, 2, GL_FLOAT, GL_FALSE, 0, (void*)0);
  glEnableVertexAttribArray(0);
  // 解除绑定
  glBindBuffer(GL_ARRAY_BUFFER, 0);
  glDrawArrays(GL_POINTS, 0, point_count / 2);
  glBindVertexArray(0);
  glDeleteVertexArrays(1, &VAO);
  glDeleteBuffers(1, &VBO);
  point_count = 0;
}

画一个三角形边框

原理

Bresenham 算法的一大特点就是可以完全不使用浮点运算，仅使用整数运算就可以绘制出一些图案。这里先尝试推导一下直线的 Bresenham 算法。

假设线段的两点为$(x_0, y_0)$和$(x_1, y_1)$，其满足$x_1-x_0>0$, $y_1-y_0 > 0$, 并且斜率$m$大于 0 小于 1。

当前点为$(x_i, y_i)$，那么下一个点可以从$(x_i + 1, y_i)$和$(x_i + 1, y_i + 1)$这两点之间选择。

根据线段在$x_i + 1$的位置上的$y$值，我们可以选择其距离较小的一点作为下一点

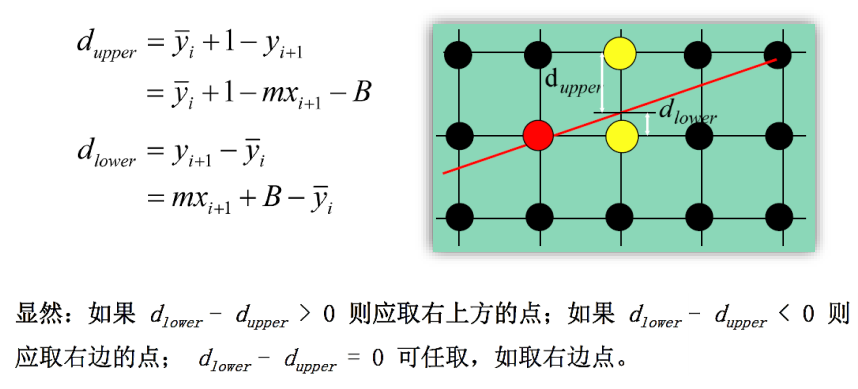
1553137846830

根据最终优化，可以得到以下算法

1553138041793

但是目前这个算法是只适应斜率大于 0 小于 1，并且满足$x_1-x_0>0$, $y_1-y_0 > 0$的情况，显然不能画出任意曲线，那么我们就需要自己变换一下。

实践

当斜率的绝对值大于 1 的时候，我们可以将 x 和 y 调换过来，就可以使得斜率的绝对值重新落在$[0, 1]$之间，最后在输出的时候再次把 x 和 y 交换过来输出。这样一来，斜率就可以控制在$[-1,1]$中

// 处理斜率大于1
bool reverse = std::abs(end_y - start_y) > std::abs(end_x - start_x);
if (reverse) {
  swap(start_x, start_y);
  swap(end_x, end_y);
}
// ...
reverse ? addPoint(y, x) : addPoint(x, y);

当$x_1-x_0<0$时，这个算法就不再是向右移动绘制，因此这种情况我们需要将线段的两个点调换过来。

// 处理反方向
if (end_x < start_x) {
  swap(start_x, end_x);
  swap(start_y, end_y);
}

经过上面两层处理之后，我们发现依然不满足$y_1-y_0 > 0$这个条件，我们可以改进一下算法，当斜率为负数的时候就将 y 的增长调整为递减。

// 处理斜率为负数
int step = start_y < end_y ? 1 : -1;
// ...
y += step;

综合以上条件和算法，最终的出来的核心代码如下：

void Points::calcLine(int start_x, int start_y, int end_x, int end_y) {
  // 处理斜率大于1
  bool reverse = std::abs(end_y - start_y) > std::abs(end_x - start_x);
  if (reverse) {
    swap(start_x, start_y);
    swap(end_x, end_y);
  }
  // 处理反方向
  if (end_x < start_x) {
    swap(start_x, end_x);
    swap(start_y, end_y);
  }
  // 处理斜率为负数
  int step = start_y < end_y ? 1 : -1;
  int y = start_y;
  int dx = end_x - start_x;
  int dy2 = 2 * std::abs(end_y - start_y);
  int dy2dx2 = dy2 - 2 * dx;
  int p = -dx;
  for (int x = start_x; x <= end_x; x++) {
    if (p <= 0) {
      p += dy2;
    } else {
      y += step;
      p += dy2dx2;
    }
    reverse ? addPoint(y, x) : addPoint(x, y);
  }
}

根据三角形的三个点，调用以上算法 3 次，画出三条直线，就可以得到一个三角形边框

// 初始化三角形顶点
triangles_vertices[0] = 10;
triangles_vertices[1] = 30;
triangles_vertices[2] = -25;
triangles_vertices[3] = 70;
triangles_vertices[4] = 33;
triangles_vertices[5] = 78;
// 画边
calcLine(triangles_vertices[0], triangles_vertices[1], triangles_vertices[2], triangles_vertices[3]);
calcLine(triangles_vertices[0], triangles_vertices[1], triangles_vertices[4], triangles_vertices[5]);
calcLine(triangles_vertices[4], triangles_vertices[5], triangles_vertices[2], triangles_vertices[3]);

为了显示出 Bresenham 的效果，这里使用$[-100, 100]$为基准坐标，显示结果如下：

1553138776427

画一个圆

原理

有了上面画三角形的经验之后，我们可以根据类似的算法画出一个圆。

根据圆的特点，我们只需要画出$\frac{1}{8}$的圆弧，根据对称翻转，就可以绘制出一整个圆来

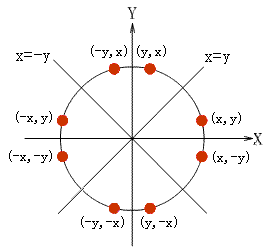
首先，我们根据中点画圆法推算一下公式

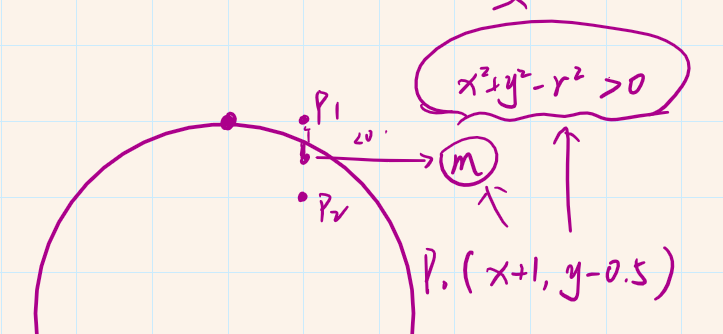
1553139100481

首先，第一个点选取圆的正上方$(0, r)$作为$(x_0, y_0)$，通过判断$(x_i + 1, y_i)$和$(x_i + 1, y_i - 1)$的中点是否在圆中，如果在圆中，那么就选择下面的点，否则就选择上面的点。而判断这个点是否在圆中可以把中点$(x_i+1, y_i - 0.5)$代入圆的公式来看结果是否小于 0。

1553141766955

最后根据 Bresenham 算法的递推方法，推算出当 P 大于 0 或者小于 0 两种更新方法。然后算出第一个点$P_0$为$1.25-r$，为了避免浮点数的运算，我们把所有的结果扩大两倍。再限制圆形半径不得小于 2，$P_0$就可以近似为$3 - 2r$

实践

最后根据对称原理，得到以下的代码

void Points::calcCircle(int cx, int cy, int r) {
  int x = 0;
  int y = r;
  int p = 3 - 2 * r;
  addPoint(cx, cy + r);
  addPoint(cx, cy - r);
  addPoint(cx + r, cy);
  addPoint(cx - r, cy);
  for (x = 1; x <= y; x++) {
    if (p < 0) {
      p += 4 * x + 6;
    } else {
      p += 4 * x - 4 * y + 10;
      y--;
    }
    addPoint(cx + x, cy + y);
    addPoint(cx + y, cy + x);
    addPoint(cx - x, cy + y);
    addPoint(cx - y, cy + x);
    addPoint(cx + x, cy - y);
    addPoint(cx + y, cy - x);
    addPoint(cx - x, cy - y);
    addPoint(cx - y, cy - x);
  }
}

渲染得到以下结果

1553142031246

GUI 控制绘画参数

和之前的一样，这里使用ImGUI来实现控制台，控制一系列的绘制参数。

具体的用法可以参照他的 Demo，这里使用Slider滑动条来控制绘制参数，可以更好地控制渲染范围。

void Points::render() {
  // 背景颜色
  glClearColor(bg_color.x, bg_color.y, bg_color.z, bg_color.w);
  glClear(GL_COLOR_BUFFER_BIT);
  // ImGui 窗口
  {
    // 工具栏
    ImGui::Begin("Draw");
    // 画布大小
    ImGui::SliderInt("Canvas Size", &canvas_size, 100, 400);
    // 点的大小
    ImGui::SliderFloat("Point Size", &point_size, 1.0, 10.0);
    // 自适应调节大小
    for (int i = 0; i < 6; i++) {
      if (triangles_vertices[i] > canvas_size) triangles_vertices[i] = canvas_size;
      if (triangles_vertices[i] < -canvas_size) triangles_vertices[i] = -canvas_size;
    }
    ImGui::RadioButton("Triangles", &draw_type, 0);
    // 使用着色器
    point_shader->Use();
    point_shader->SetColor("pointColor", shader_color);

    if (draw_type == 0) {
      ImGui::Checkbox("Rasterize", &rasterize);

      ImGui::Columns(3, "triangles");
      ImGui::Separator();

      ImGui::Text("Point 1: ");
      ImGui::SliderInt("X1", &triangles_vertices[0], -canvas_size, canvas_size);
      ImGui::SliderInt("Y1", &triangles_vertices[1], -canvas_size, canvas_size);
      ImGui::NextColumn();

      ImGui::Text("Point 2: ");
      ImGui::SliderInt("X2", &triangles_vertices[2], -canvas_size, canvas_size);
      ImGui::SliderInt("Y2", &triangles_vertices[3], -canvas_size, canvas_size);
      ImGui::NextColumn();

      ImGui::Text("Point 3: ");
      ImGui::SliderInt("X3", &triangles_vertices[4], -canvas_size, canvas_size);
      ImGui::SliderInt("Y3", &triangles_vertices[5], -canvas_size, canvas_size);
      ImGui::NextColumn();

      ImGui::Columns(1);
      ImGui::Separator();
      // 画边
      calcLine(triangles_vertices[0], triangles_vertices[1], triangles_vertices[2], triangles_vertices[3]);
      calcLine(triangles_vertices[0], triangles_vertices[1], triangles_vertices[4], triangles_vertices[5]);
      calcLine(triangles_vertices[4], triangles_vertices[5], triangles_vertices[2], triangles_vertices[3]);
      // 光栅化
      if (rasterize) {
        calcTriangle();
      }
      drawPoint();
    }

    ImGui::RadioButton("Circle", &draw_type, 1);

    if (draw_type == 1) {
      ImGui::PushItemWidth(120);
      ImGui::SliderInt("X", &circle_x, -canvas_size, canvas_size); ImGui::SameLine();
      ImGui::SliderInt("Y", &circle_y, -canvas_size, canvas_size); ImGui::SameLine();
      ImGui::SliderInt("R", &circle_r, 2, canvas_size);
      if (circle_r > canvas_size) circle_r = canvas_size;
      ImGui::PopItemWidth();
      // 画圆
      calcCircle(circle_x, circle_y, circle_r);
      drawPoint();
    }

    ImGui::ColorEdit3("Point color", (float*)& shader_color);
    ImGui::ColorEdit3("Background color", (float*)& bg_color);
    ImGui::Text("Application average %.3f ms/frame (%.1f FPS)", 1000.0f / ImGui::GetIO().Framerate, ImGui::GetIO().Framerate);
    ImGui::End();
  }
}

通过调节三角形三个顶点的位置来控制三角形的绘制：

gif

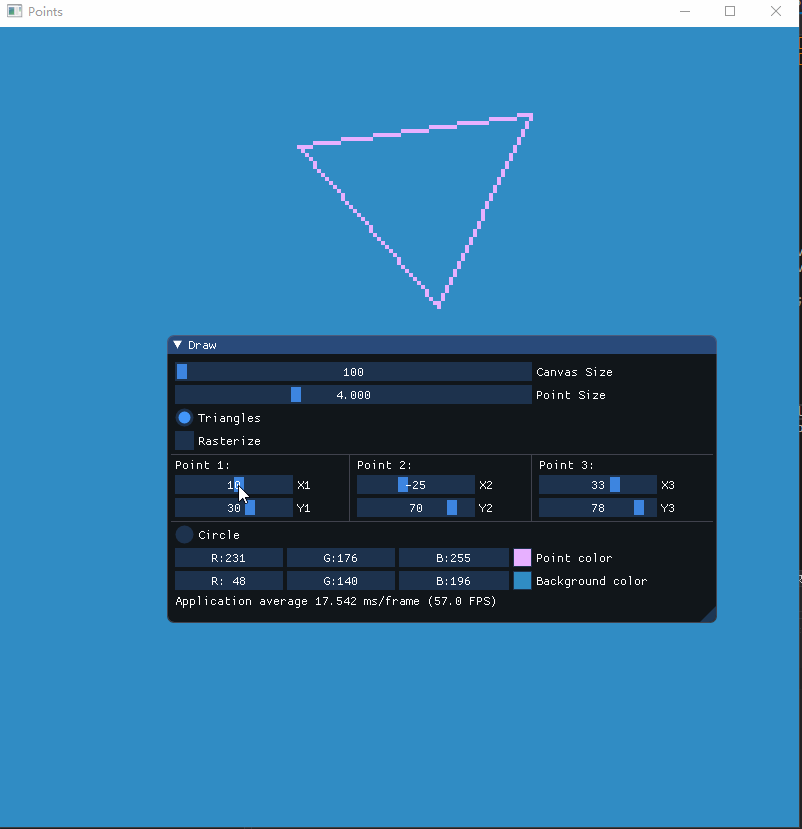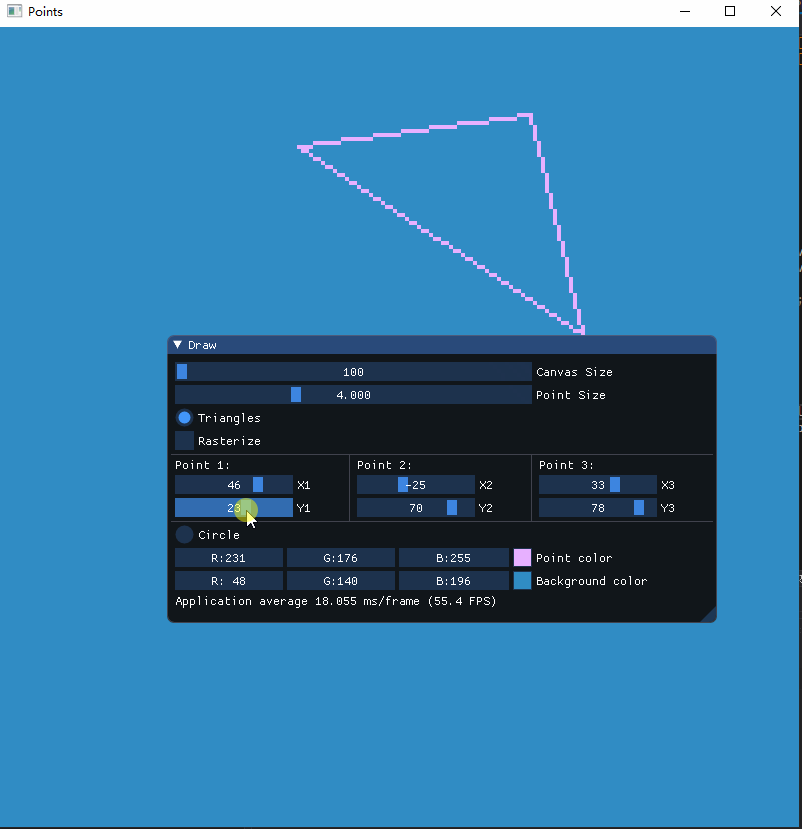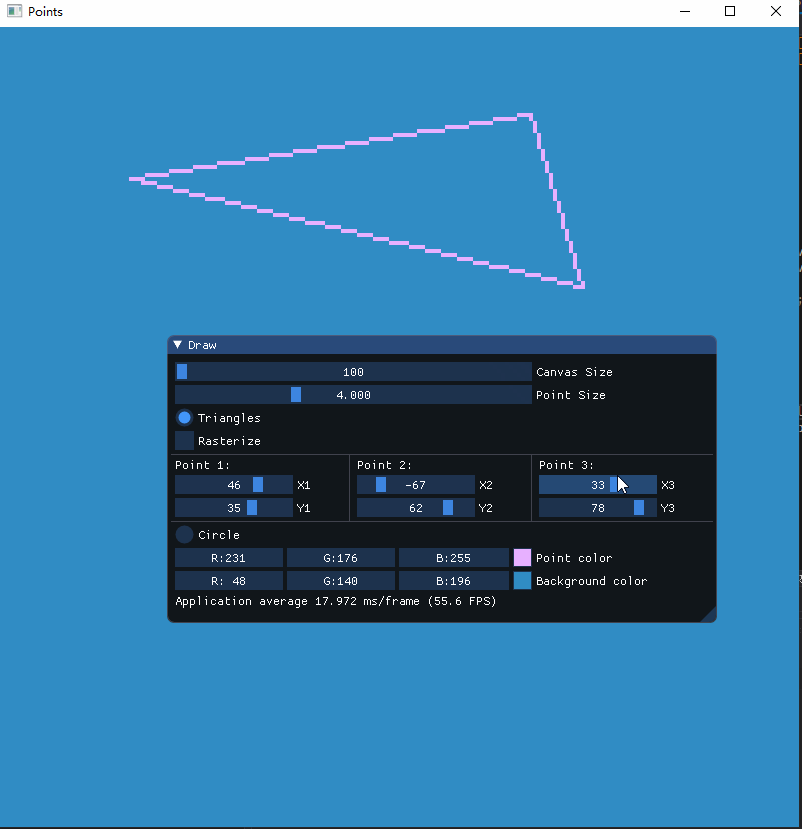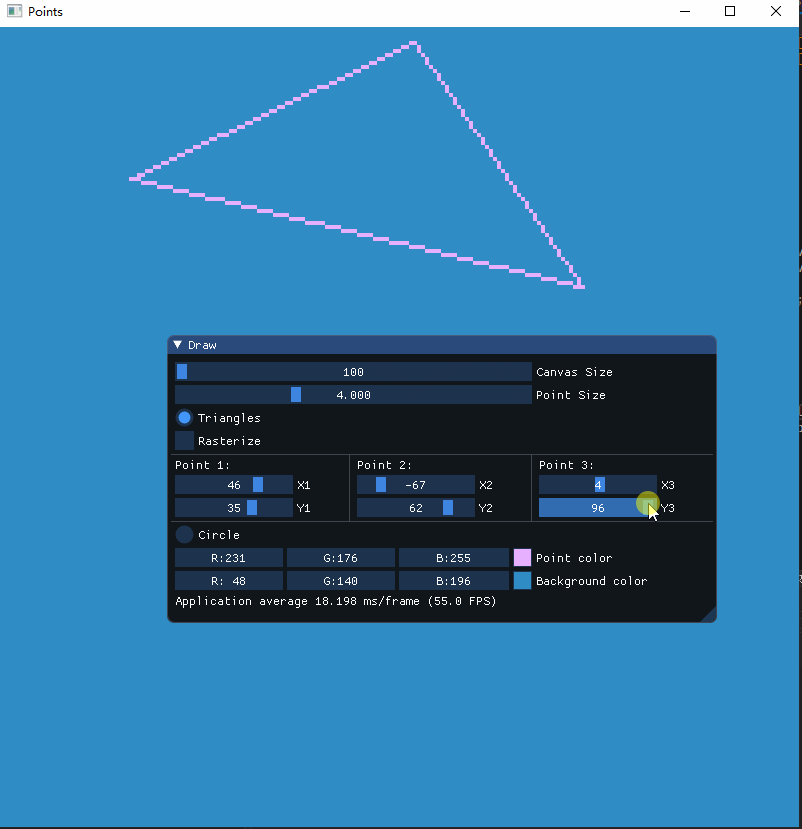
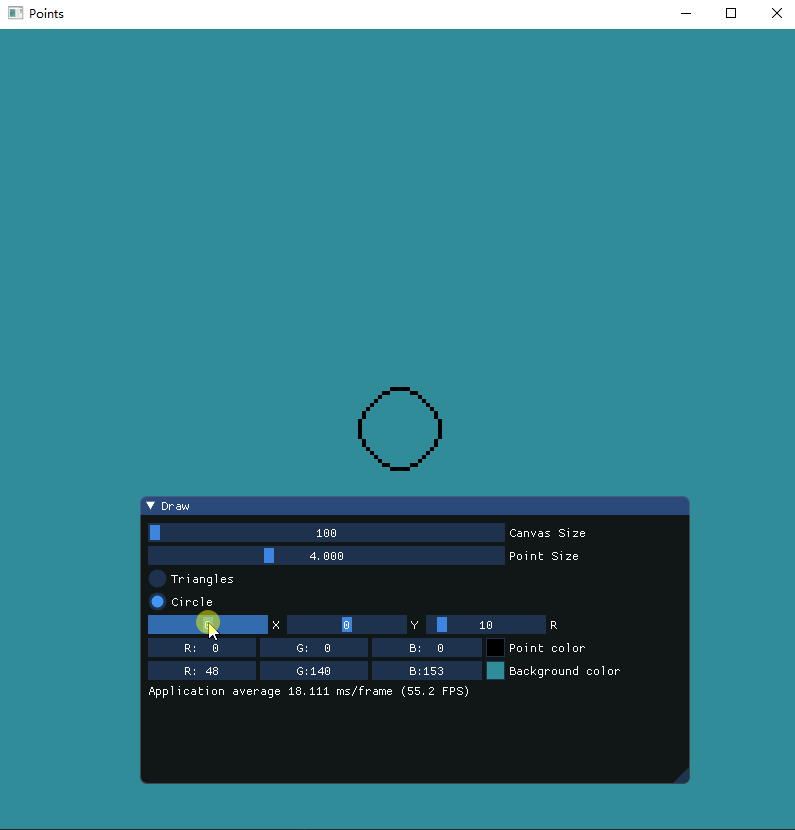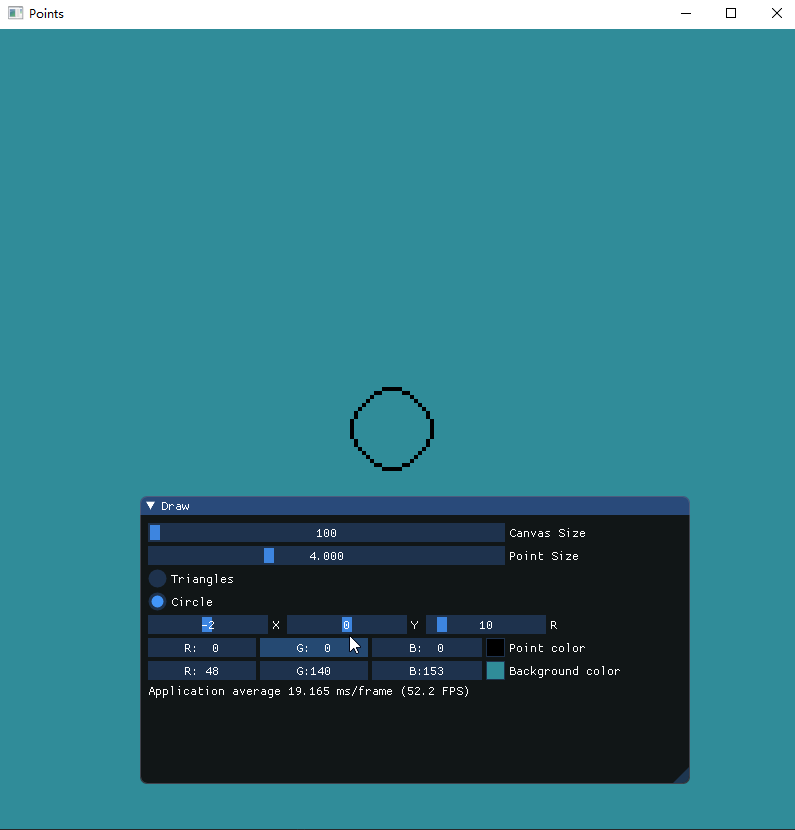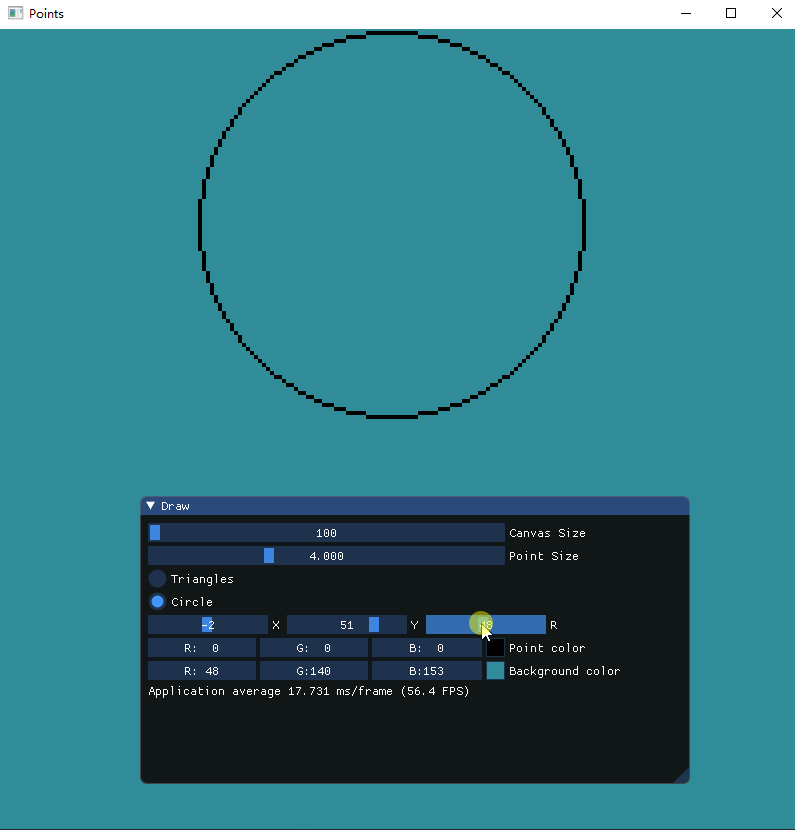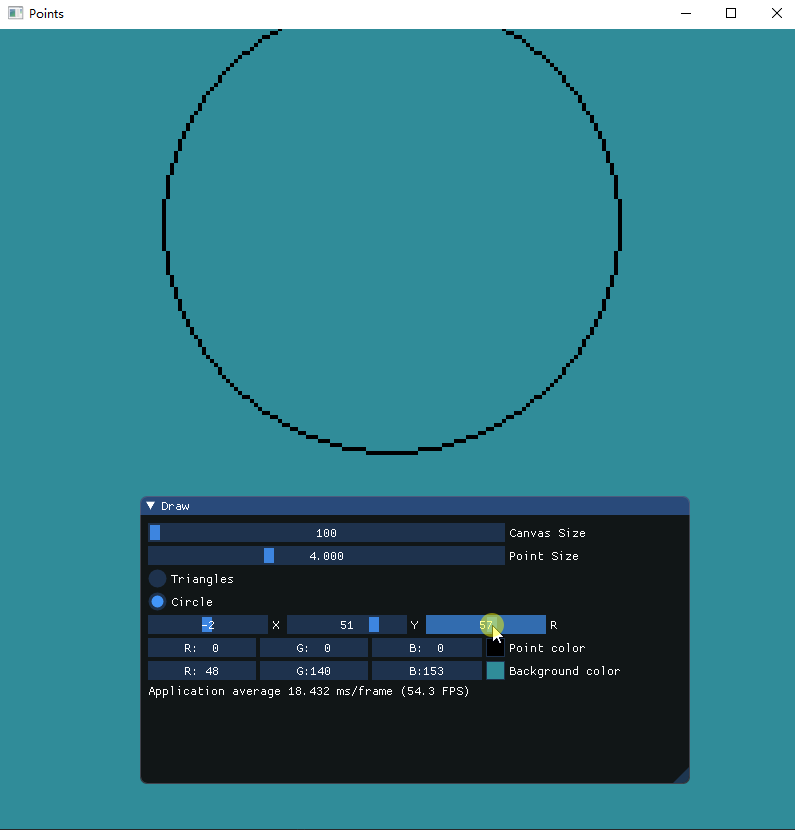
通过控制圆形位置和半径大小来绘制圆

circle

三角形光栅转换算法

原理

三角形的光栅化有多种算法，这里使用 Edge Equations 算法来实现光栅化

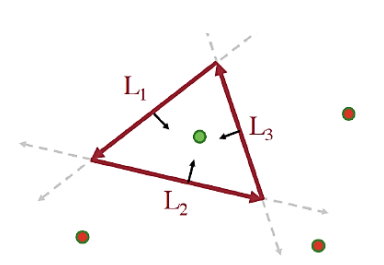
1553142691754

这个算法的核心就在于算出三角形三条边的直线方程，然后判断点是否再三角形的内部然后决定是否对其进行填充。

直线方程可以使用直线的两点式来求出$Ax+By+C$中的 ABC 参数

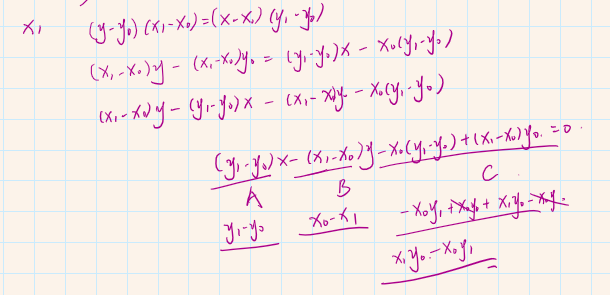
1553143139334

然后，我们需要对直线进行中心化，确保三角形内所有点代入结果都是为正，这个可以通过把三角形的第三个点代入当前直线，如果结果为负数那么就把 ABC 参数全部取反。

确定了直线方程之后，还需要找出所需要遍历的点，这就要找出三角形的一个 bounding box

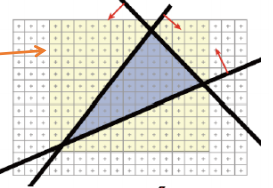
1553142870143

这里就简单的根据三个点找出其 x 和 y 的最大值和最小值，构成一个矩形，然后对这个矩形里面的所有点进行判断。

实践

根据上面的原理，可以得到以下代码

void Points::calcTriangle() {
  // 计算直线方程
  int parameter[9];
  parameter[0] = triangles_vertices[5] - triangles_vertices[3];
  parameter[1] = triangles_vertices[2] - triangles_vertices[4];
  parameter[2] = triangles_vertices[3] * triangles_vertices[4] - triangles_vertices[2] * triangles_vertices[5];

  parameter[3] = triangles_vertices[5] - triangles_vertices[1];
  parameter[4] = triangles_vertices[0] - triangles_vertices[4];
  parameter[5] = triangles_vertices[1] * triangles_vertices[4] - triangles_vertices[0] * triangles_vertices[5];

  parameter[6] = triangles_vertices[3] - triangles_vertices[1];
  parameter[7] = triangles_vertices[0] - triangles_vertices[2];
  parameter[8] = triangles_vertices[1] * triangles_vertices[2] - triangles_vertices[0] * triangles_vertices[3];

  // 中心化
  for (int i = 0; i < 3; i++) {
    if (parameter[i * 3] * triangles_vertices[i * 2] + parameter[i * 3 + 1] * triangles_vertices[i * 2 + 1] + parameter[i * 3 + 2] < 0) {
      for (int j = 0; j < 3; j++) {
        parameter[i * 3 + j] *= -1;
      }
    }
  }

  // 计算方块
  int max_x = triangles_vertices[0];
  int min_x = triangles_vertices[0];
  int max_y = triangles_vertices[1];
  int min_y = triangles_vertices[1];
  for (int i = 0; i < 3; i++) {
    if (triangles_vertices[i * 2] > max_x) max_x = triangles_vertices[i * 2];
    if (triangles_vertices[i * 2] < min_x) min_x = triangles_vertices[i * 2];
    if (triangles_vertices[i * 2 + 1] > max_y) max_y = triangles_vertices[i * 2 + 1];
    if (triangles_vertices[i * 2 + 1] < min_y) min_y = triangles_vertices[i * 2 + 1];
  }

  for (int x = min_x; x <= max_x; x++) {
    for (int y = min_y; y <= max_y; y++) {
      bool inside = true;
      for (int i = 0; i < 3; i++) {
        if (parameter[i * 3] * x + parameter[i * 3 + 1] * y + parameter[i * 3 + 2] < 0) {
          inside = false;
          break;
        }
      }
      if (inside) {
        addPoint(x, y);
      }
    }
  }
}

最后得到以下结果，通过调节绘制的点的大小，可以清晰地看见三角形内部完全是由点来填充的

edge

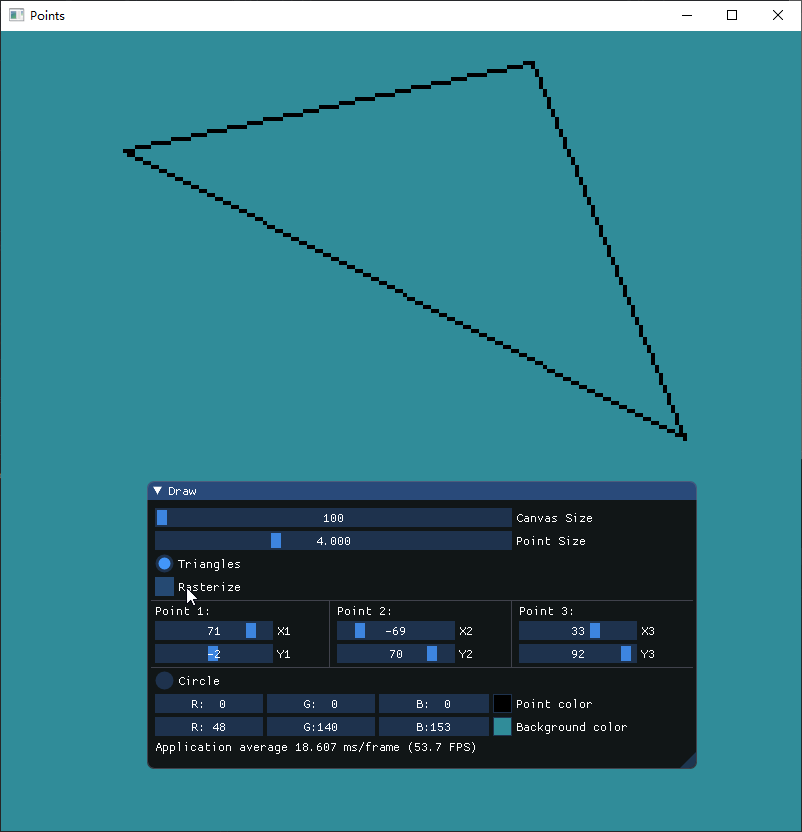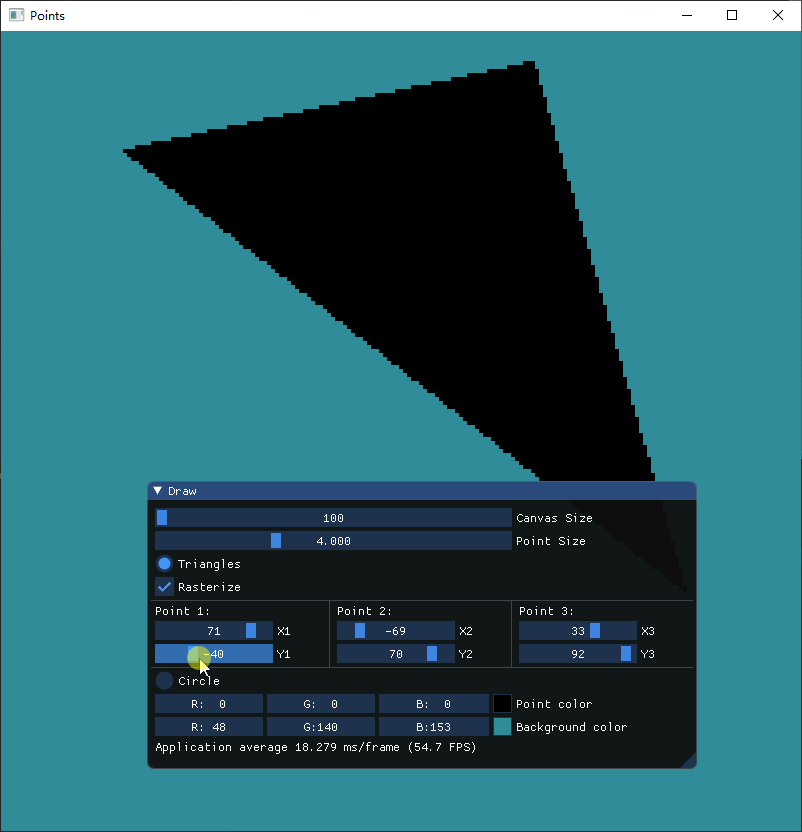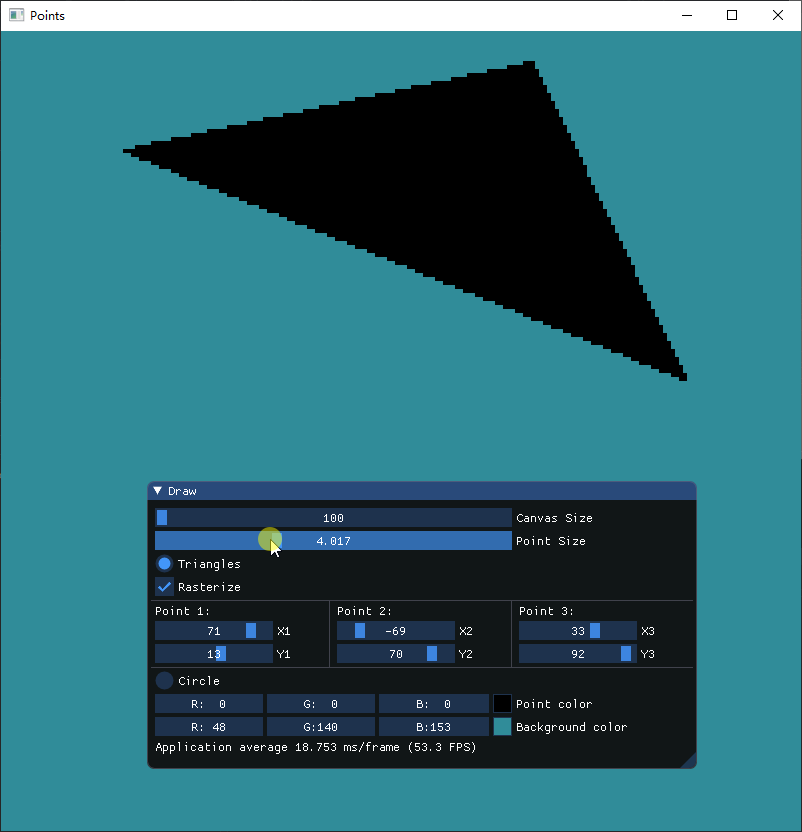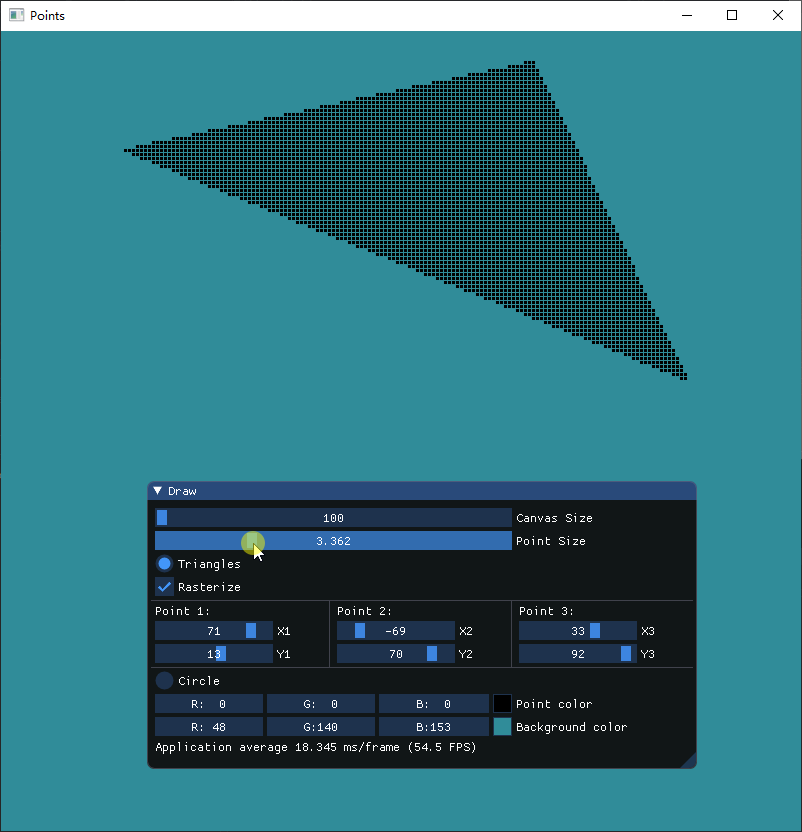
结语

如果还有不太明白的地方可以到这里查看完整的代码。

通过这次学习，了解了 Bresenham 算法的美妙之处，这是计算机图形学中的一个非常重要的算法，极大了优化了计算的效率。至于三角形的光栅化其实还有 Edge Walking 等其他算法，这里只是介绍了其中的一种比较简单的算法，不过根据这个算法已经可以扩展出非常多的用法。

这些算法都是图形学的基础，虽然现在我们不需要自己实现这些算法，这些算法早已经集成在硬件层面了，但是这种思想可以扩展到很多地方去。