🎨 CG | OpenGL 中的摄像机

​ 之前在 OpenGL 中，已经创建了各种形状，这一次来创建一个摄像机，使得我们可以任意移动，从各个角度观察创建的物理。虽然 OpenGL 本身没有摄像机(Camera)的概念，但我们可以通过把场景中的所有物体往相反方向移动的方式来模拟出摄像机，产生一种我们在移动的感觉，而不是场景在移动。

🚀 代码: Github

🔗 参考链接：https://learnopengl.com/Getting-started/Camera

投影(Projection)

把上次绘制的 cube 放置在(-1.5, 0.5, -1.5)位置，要求 6 个面颜色不一致

在上次实验中，已经描述了如何画出一个立方体，这里就不再详细说明

为了可以看出来这是一个立方体，这里把摄像机视角调成(6, 9, 21),即从立方体的右上方观察

正交投影(orthographic projection)

实现正交投影，使用多组(left, right, bottom, top, near, far)参数， 比较结果差异

实现正交投影比较简单，只需要使用glm::ortho函数，然后传入left, right, bottom, top, near, far参数，通过 shader 设置到位置上，就可以实现正交投影。

projection = glm::ortho(
  this->orthographicValue[0], this->orthographicValue[1],
  this->orthographicValue[2], this->orthographicValue[3],
  this->orthographicValue[4], this->orthographicValue[5]);

下面使用基本的参数来测试一下：

下面来调整一下参数

首先是上下左右

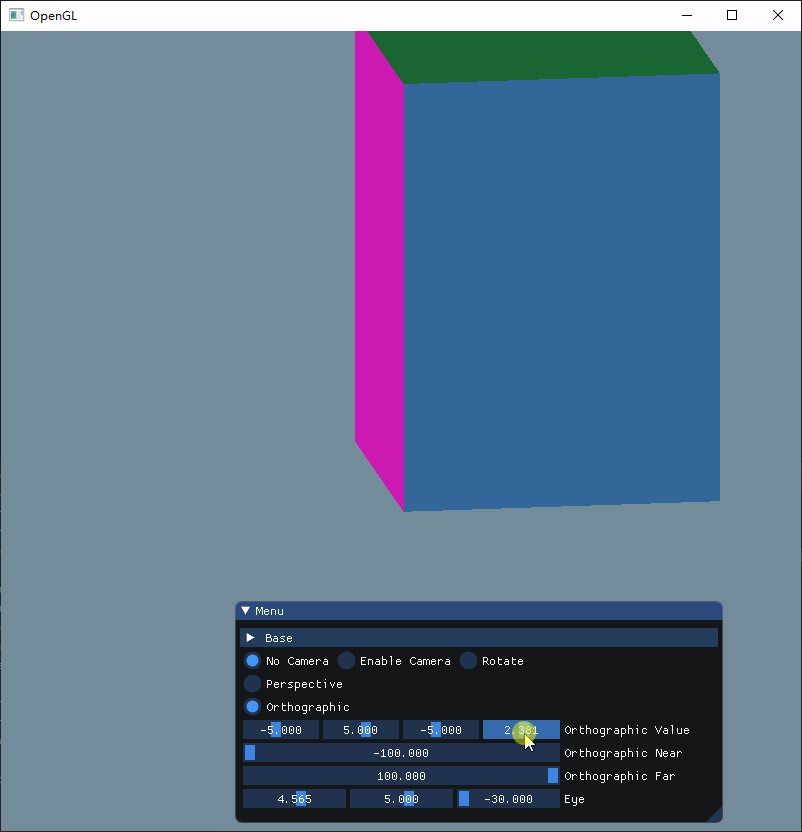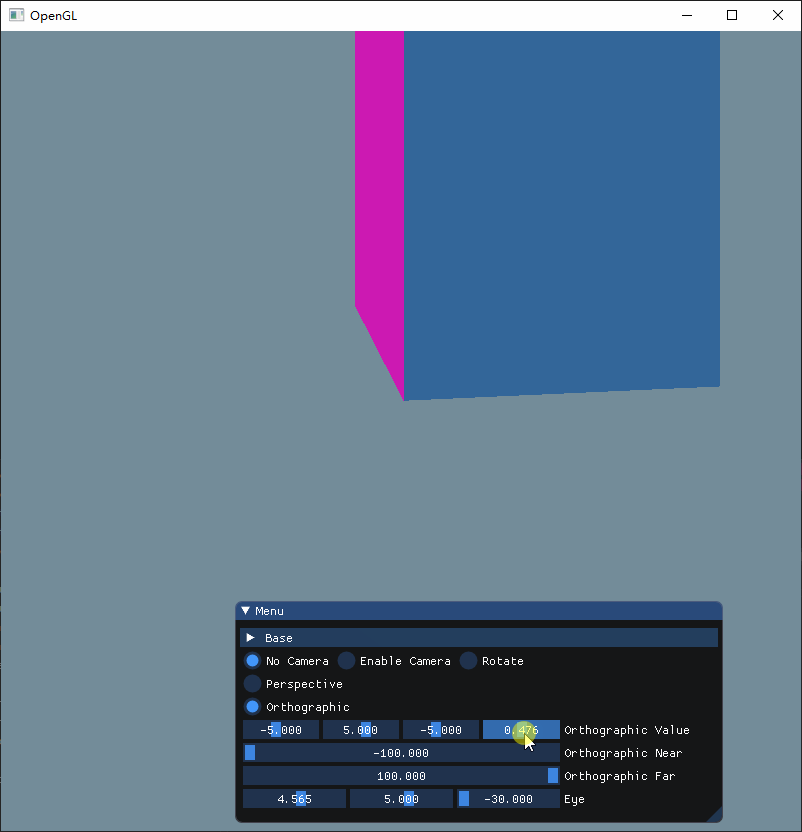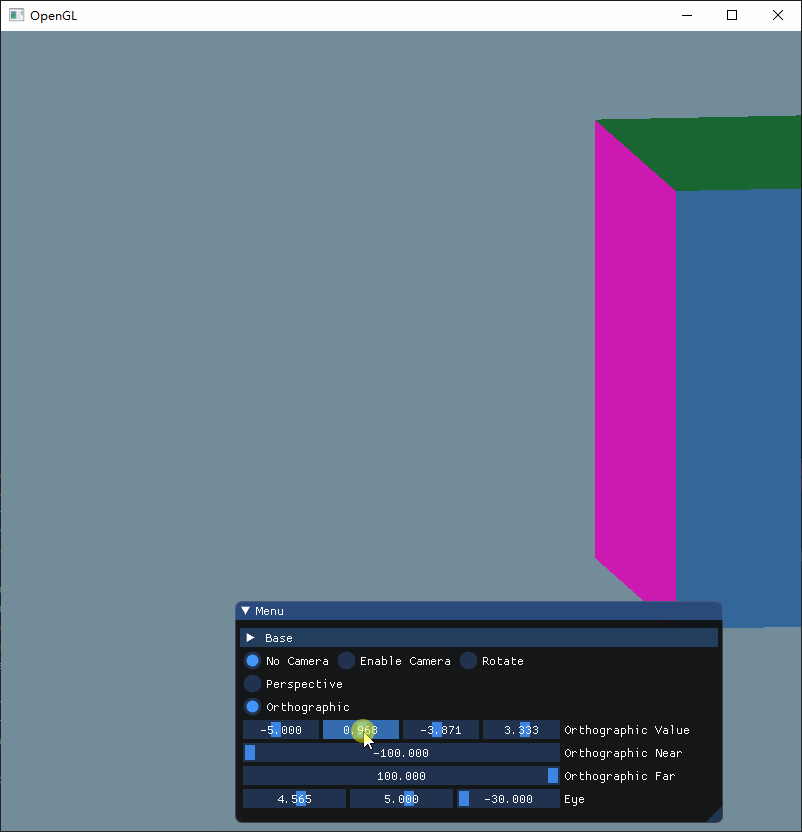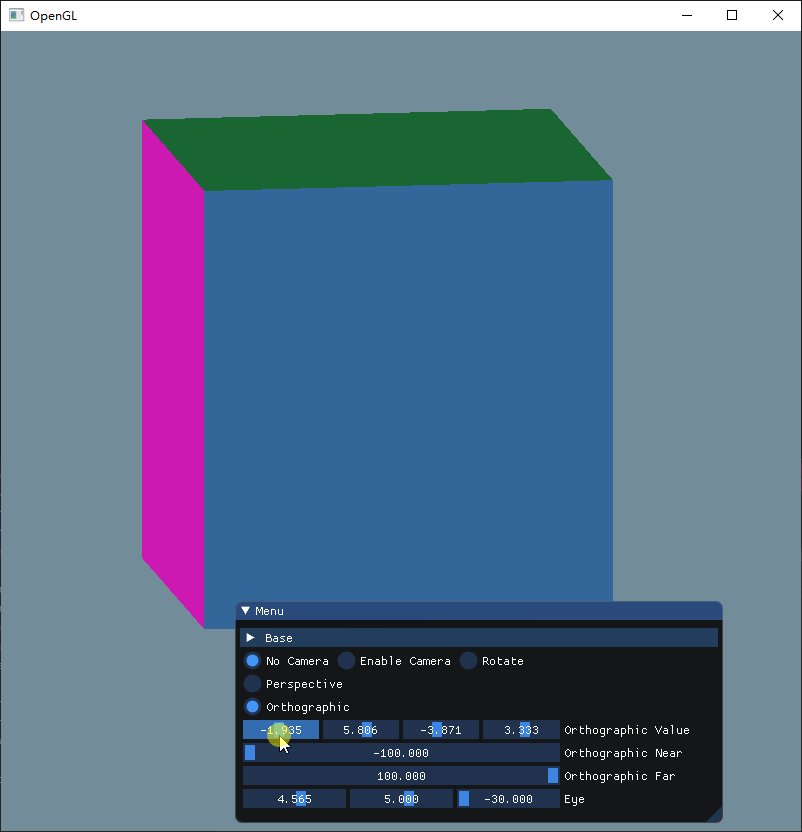
可以看出，前四个参数依次制定了投影锥体的左右下上边界

下面我们把视角调成正面，再来看看不同参数会导致什么效果，以及分析其具体原因。

参数	图片
(-5,5,-5,5)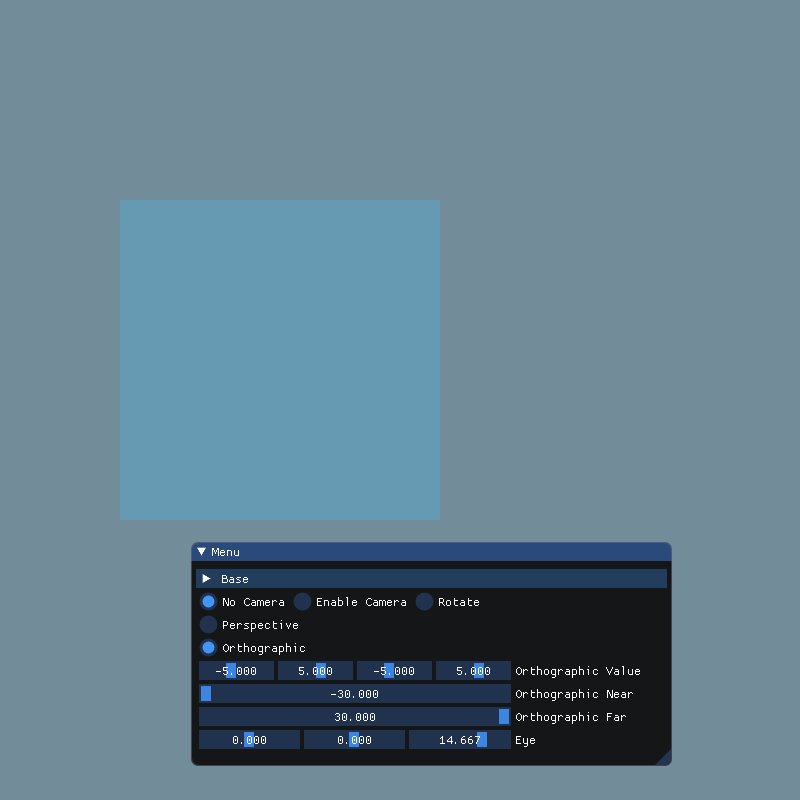
(-3.5, 3.5, -3.5, 3.5)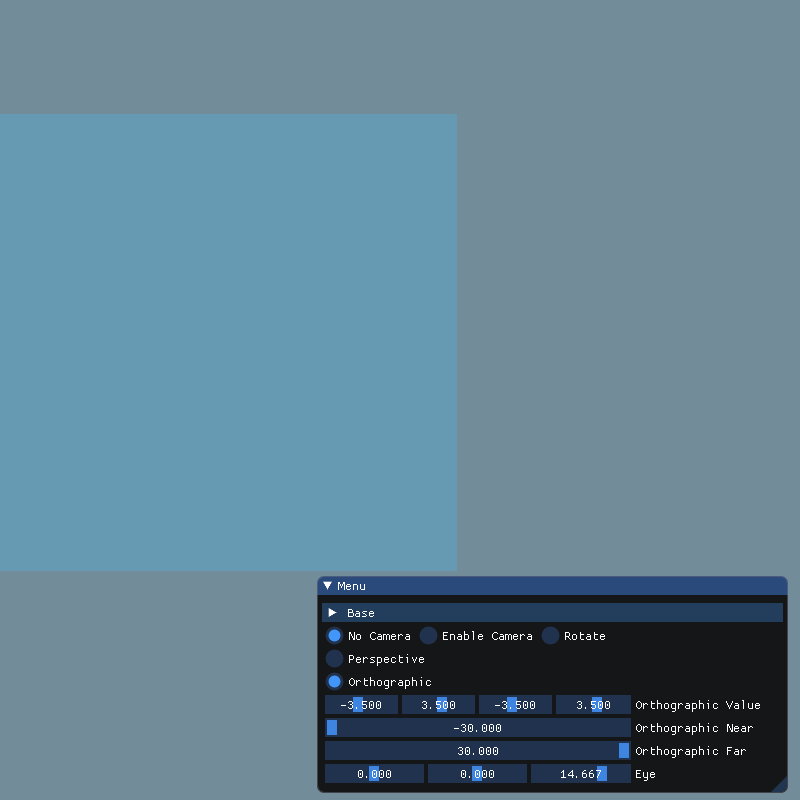
(-4, 1, -2, 10)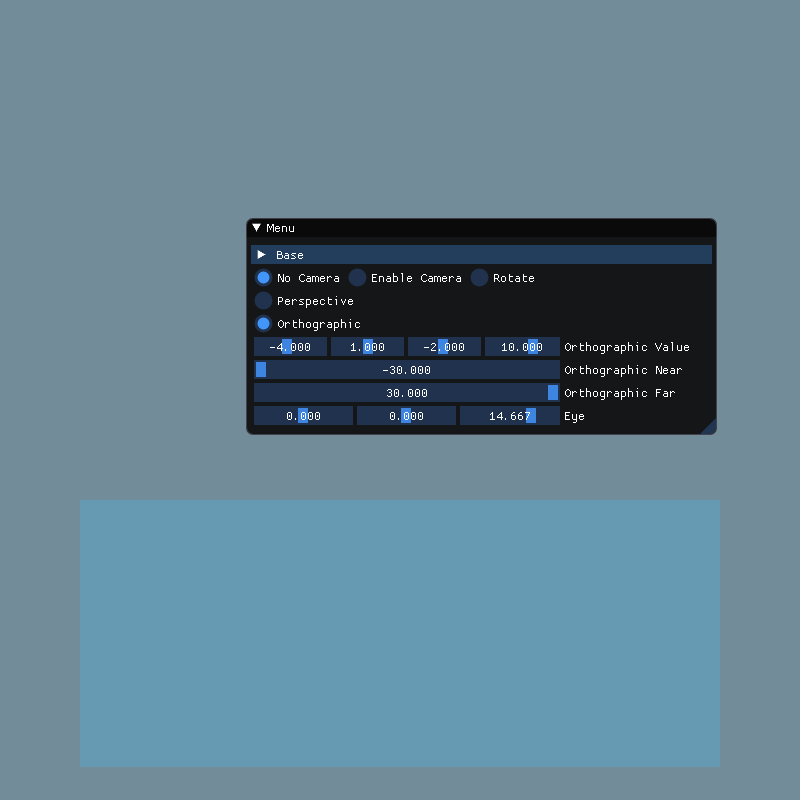

把视图调成(-5,5,-5,5)的时候，可以很清晰地看到，立方体的正面的中心是处于(-1.5, 0.5)的，这也符合一开始设定的坐标(-1.5, 0.5, -1.5)

然后把视图调成(-3.5, 3.5, -3.5, 3.5)，因为立方体的边长为 4，因此立方体的正面的左边也正好落在x = -3.5的位置上，从图中可以看到，这时立方体正面的左边刚好和视图左边重合。

当然，我们同样可以把视图调成非正方体，这样，正方形投影到 2D 平面上就成为了长方形

那么，剩下两个参数near和far又是什么呢?

如果把视图调整在立方体的正面，我们只能看到立方体的正面的背面在不同的值情况下不断闪现

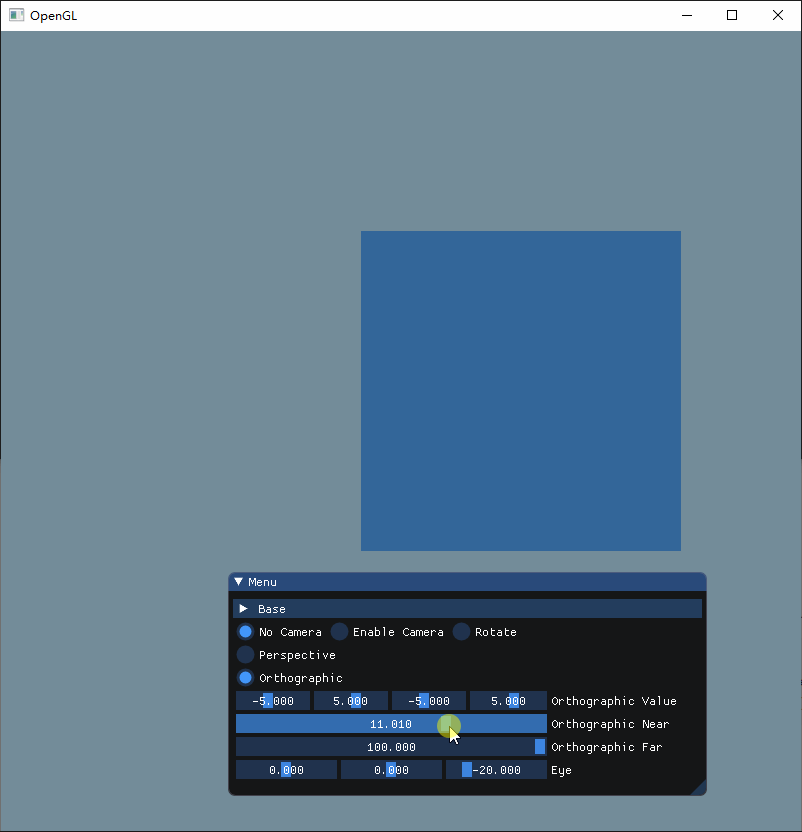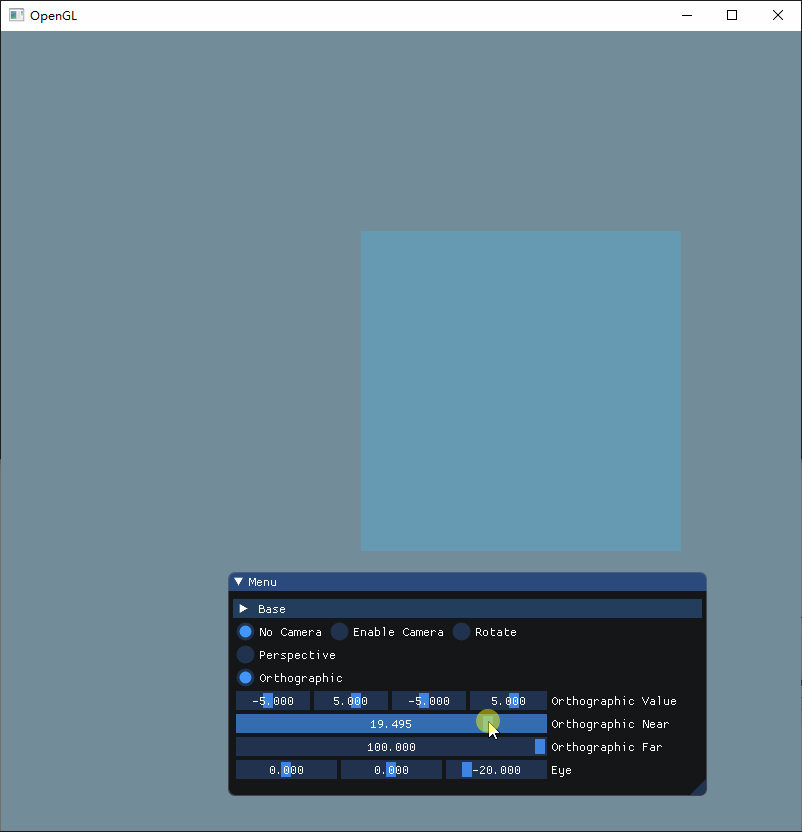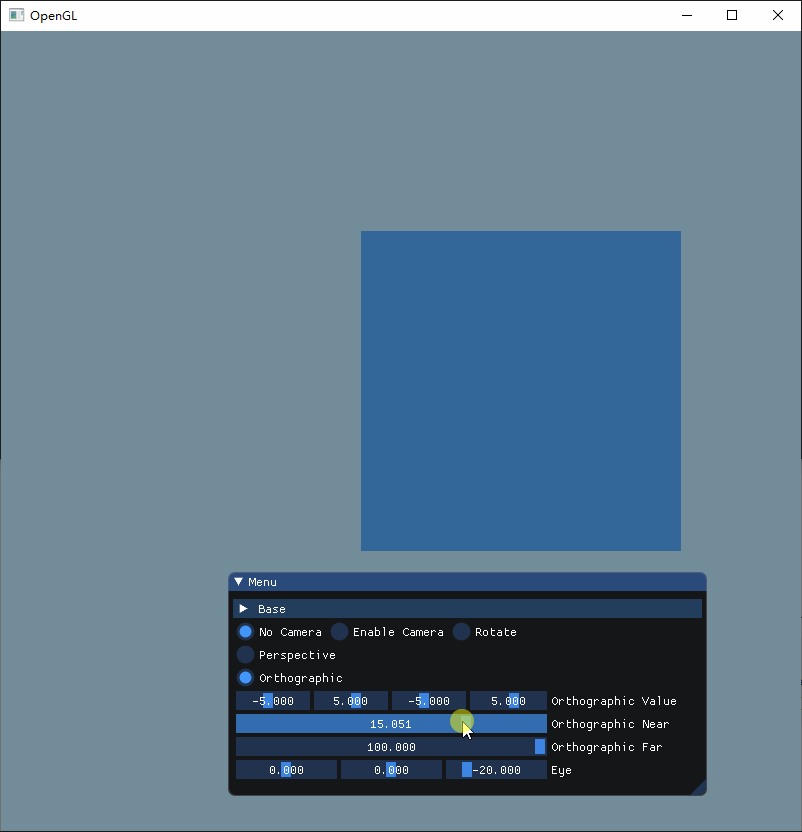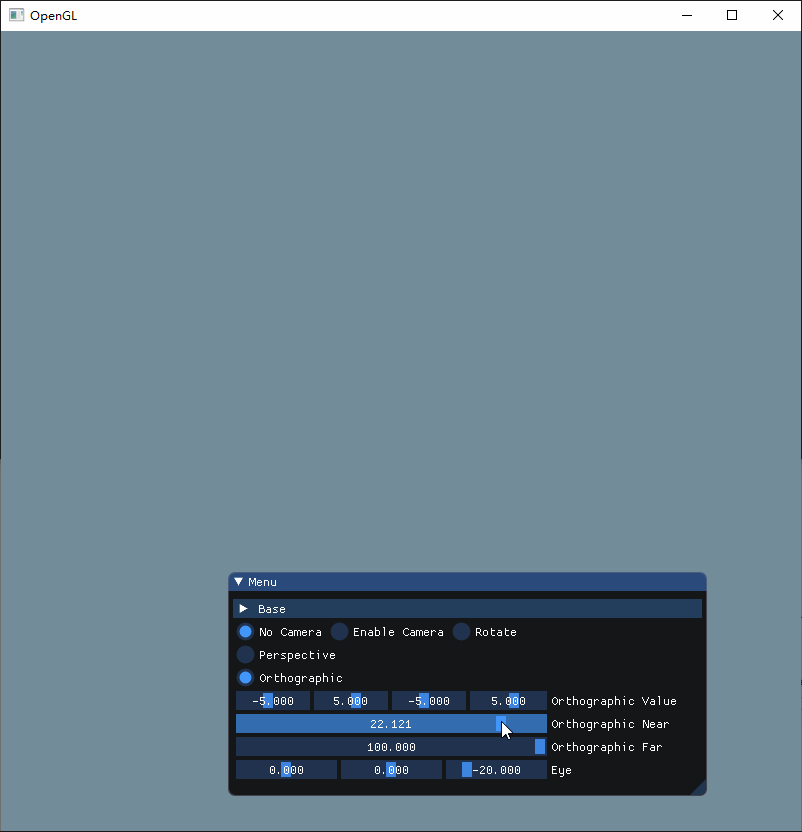
为了直观感受这两个参数的作用，现在把视角调成立体再来看看

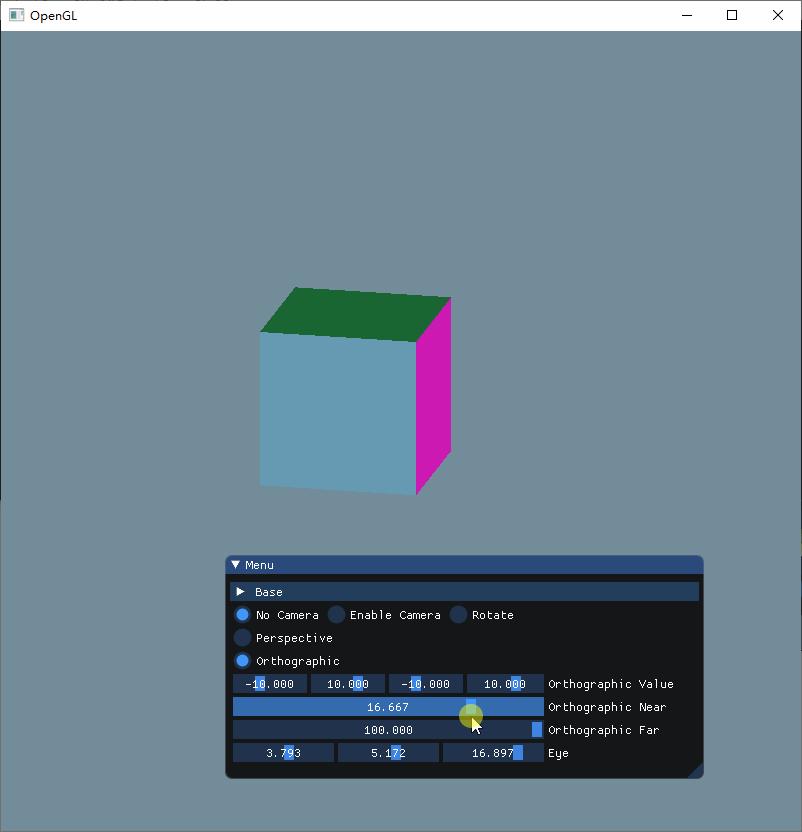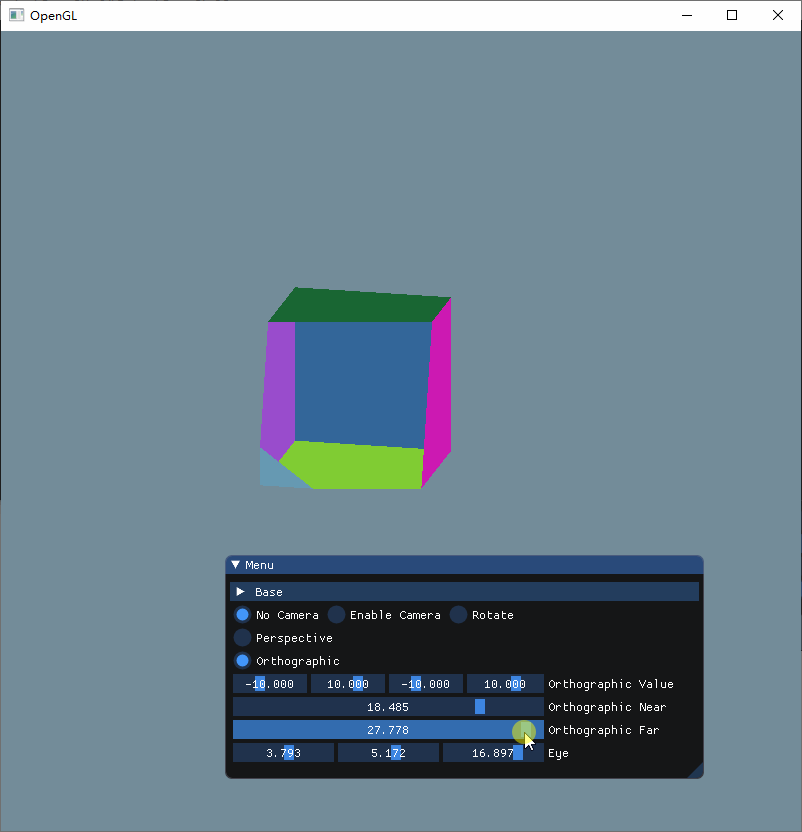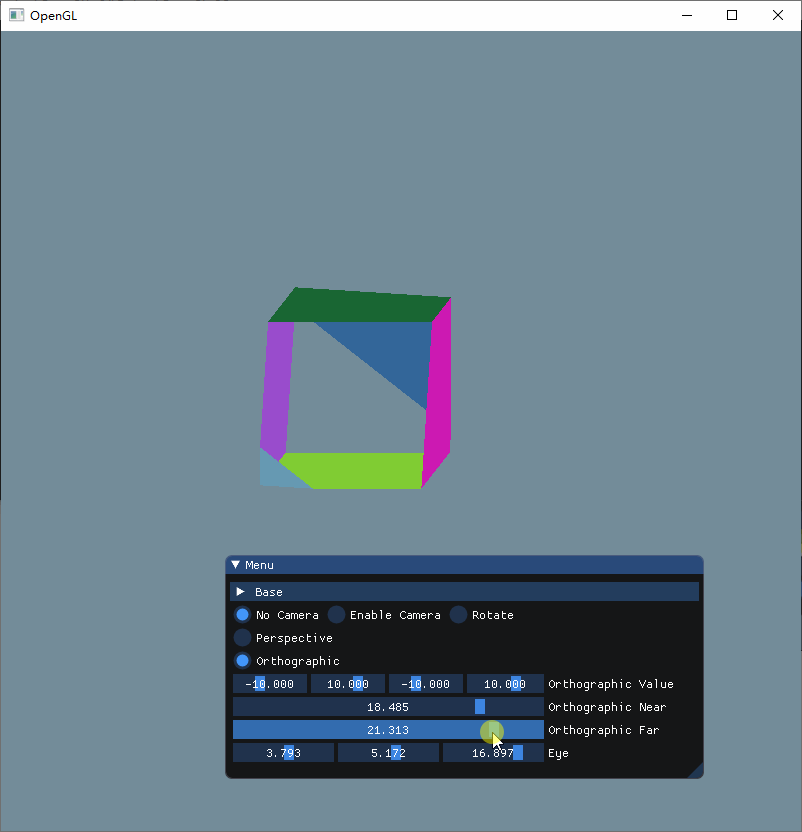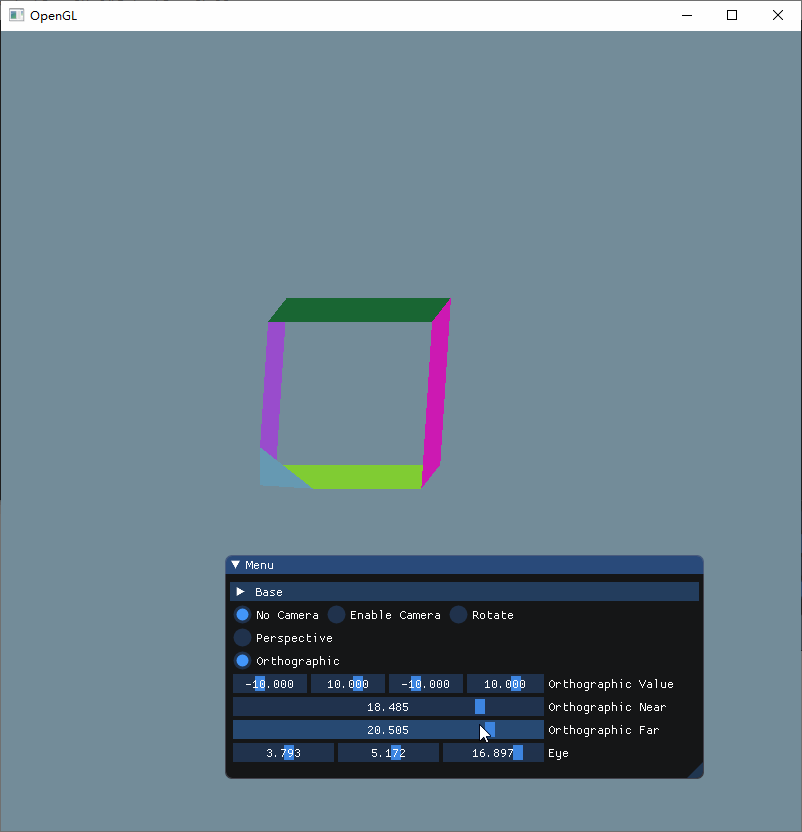
这次可以很清晰看到，Near和Far其实就是决定着Z轴显示的内容，当我们把Near增大的时候，可以看到立方体的前方部分被切割掉了，而把Far调小的时候, 立方体的后方就会被切割，而把两者都分别调小和增大的时候，就可以显示整个立方体。

因此，这两个参数就是近裁剪平面和远裁剪平面，只有在这两个平面之内内容才会被投影到屏幕上

透视投影(perspective projection)

实现透视投影，使用多组参数，比较结果差异

透视投影的实现与正交投影类似，只需使用glm::perspective定义投影矩形即可

projection = glm::perspective(
  glm::radians(this->perspectiveValue[0]), this->perspectiveValue[1],
  this->perspectiveValue[2], this->perspectiveValue[3]);

透视投影有四个参数，分别是fovy,aspect, near和far

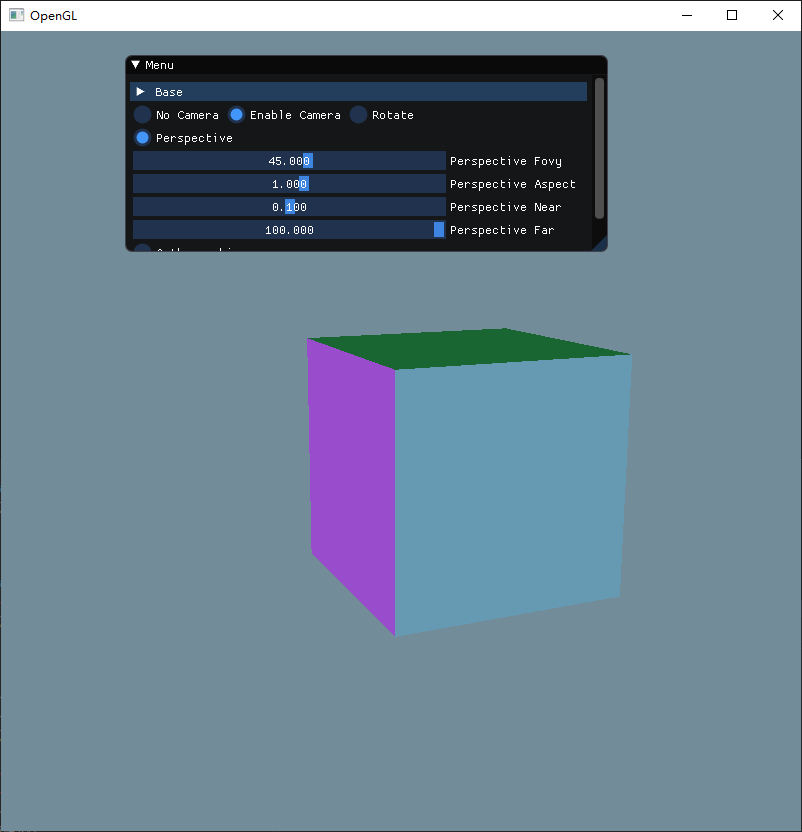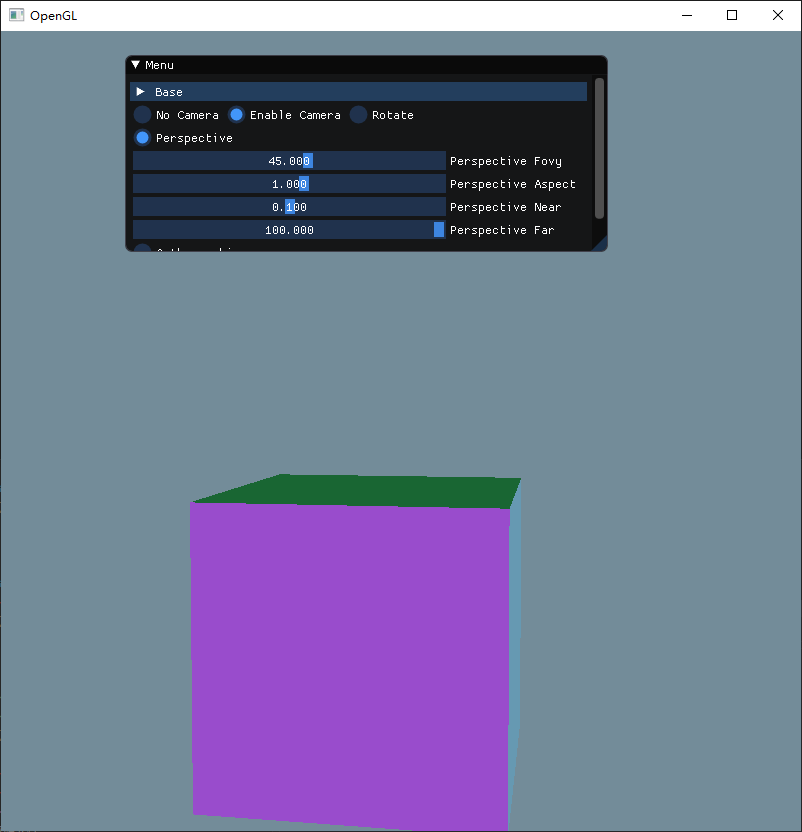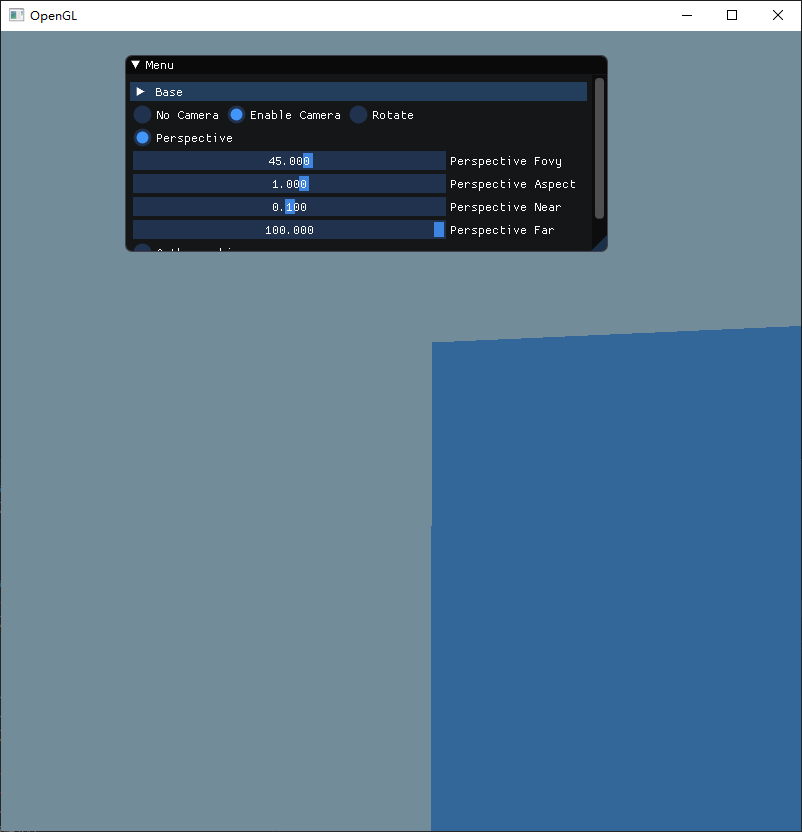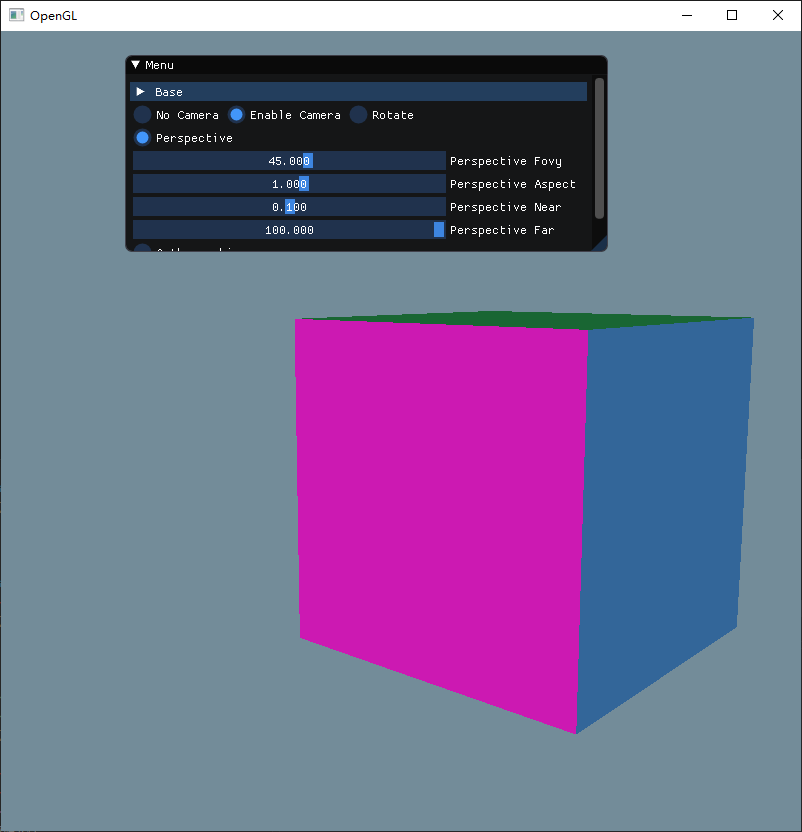
第一个参数fovy要求传入的是弧度，因此需要在外部加一层radians处理，然后来调节一下这个参数，看看会发生什么变化。

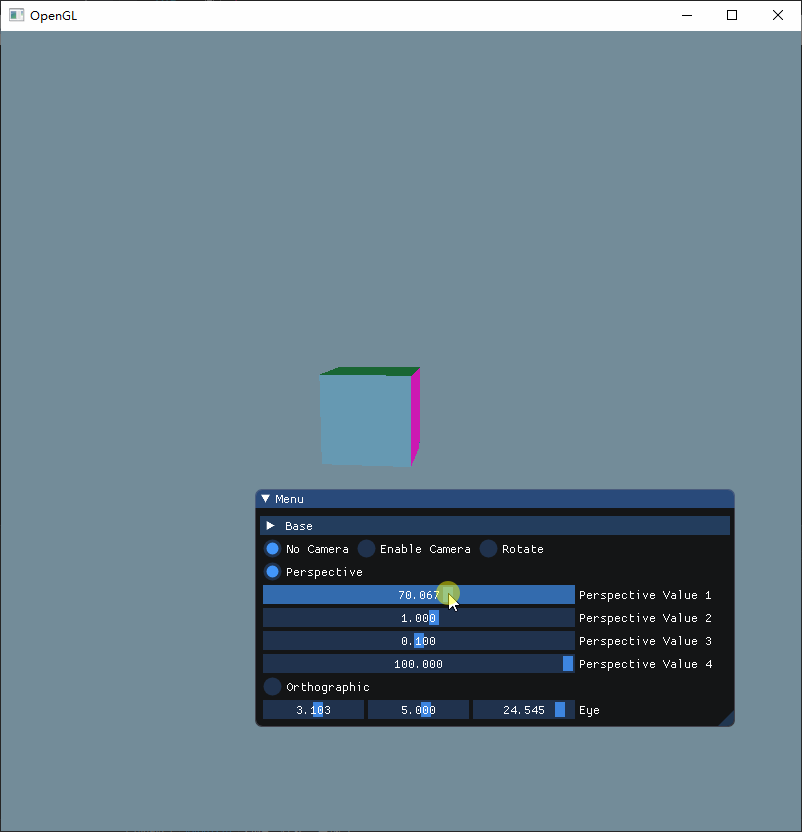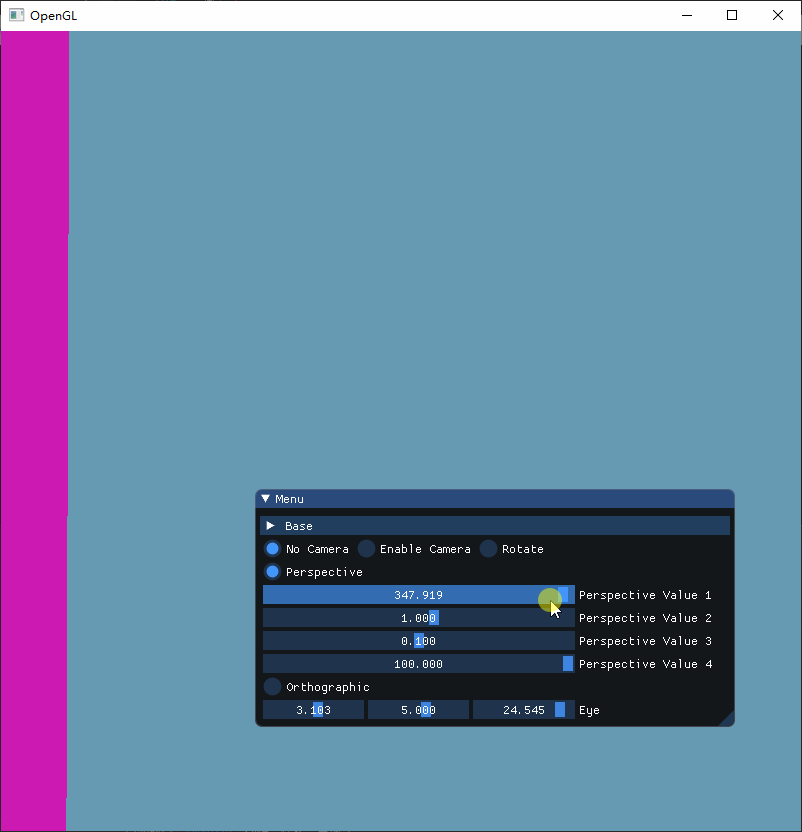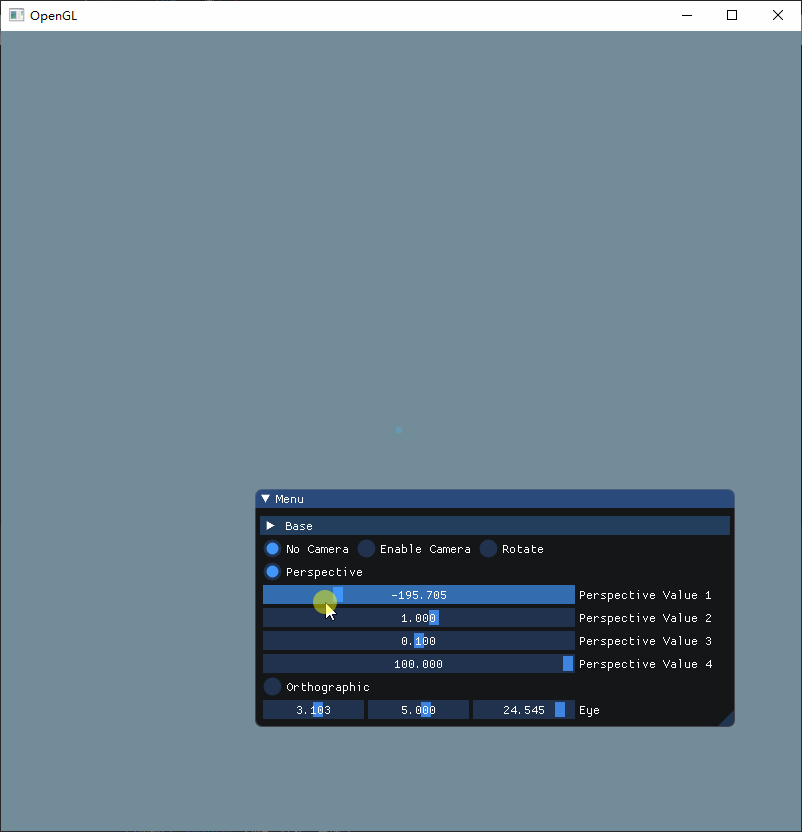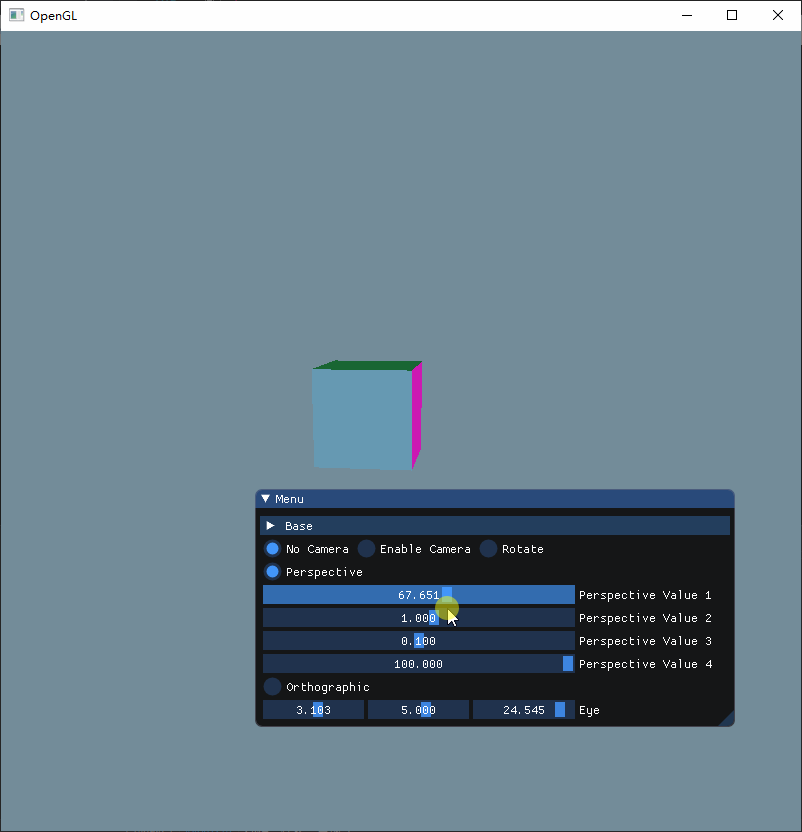
从上图可以看到，当弧度接近 180 度的时候，立方体会变得越小，而当弧度是负数的时候，立方体就会变成反方向地变小，弧度越接近 0，那么立方体就会越大，而为 0 的时候刚好消失。

因此可以推断，这个参数正是对应透视投影的角度

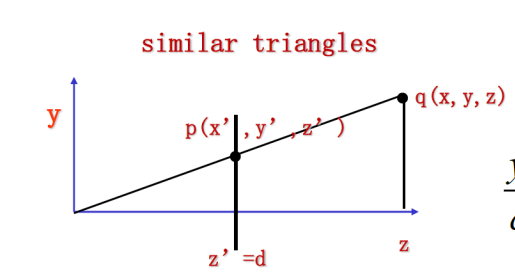
根据透视投影的原理，这个投影的三角形的角度会直接影响到投影物投影到屏幕上的大小，当达到这个三角形的oqz这个角趋近于 0 的时候，投影的视图也会无限地放大，也对应了上面的现象。

从另一个角度来看，也可以理解为是摄像机的视角，当视角变大的时候，所看到的物体就会变小。

然后再看第二个参数aspect

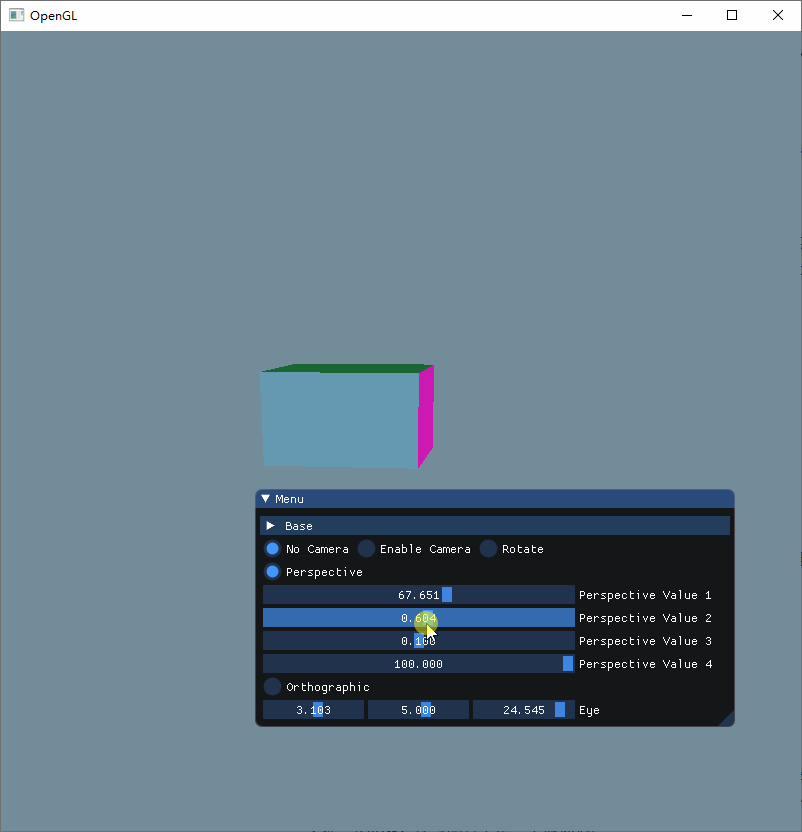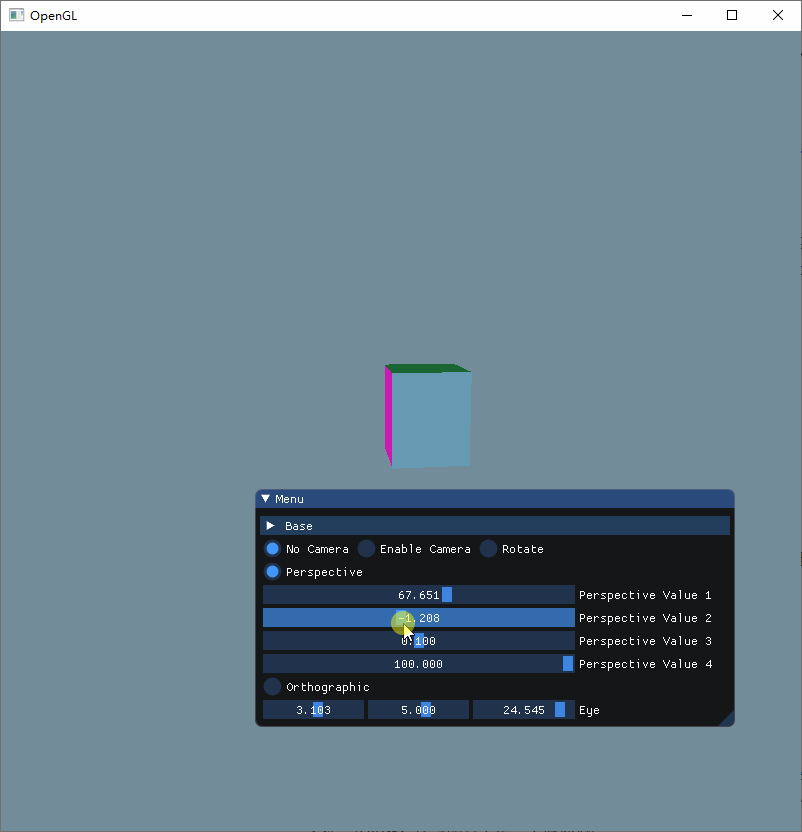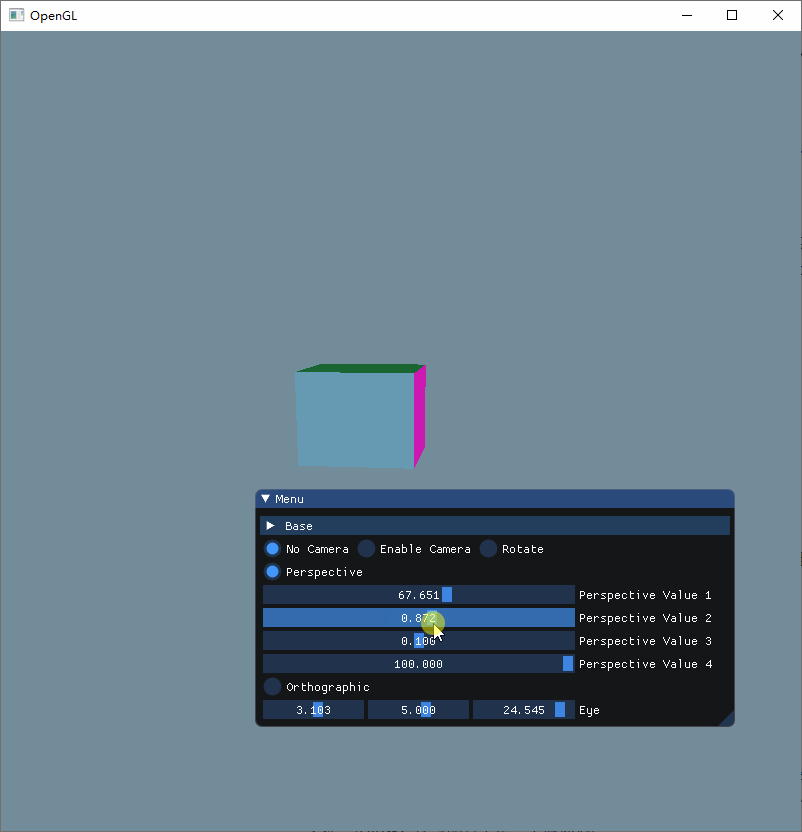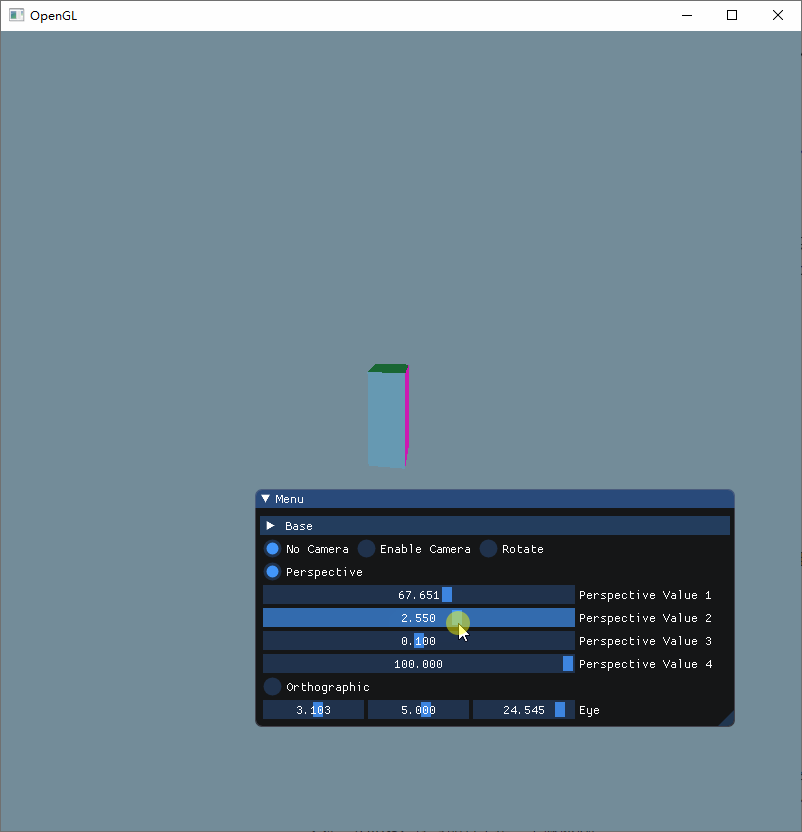
可以看出来

当aspect为 1 的时候，物体按正常的比例进行显示

当aspect大于 0 并且小于 1 的时候，值越趋近于 0，立方体就被拉伸得越多

当aspect大于 1 的时候，值越大，立方体就会被压缩得更多

可以得知，这个参数是控制着物体的纵横比，因为我设置的屏幕大小为800x800，因此 1：1 的时候刚好按正常比例显示。

和正交投影一样的是，透视投影也有near和far两个参数

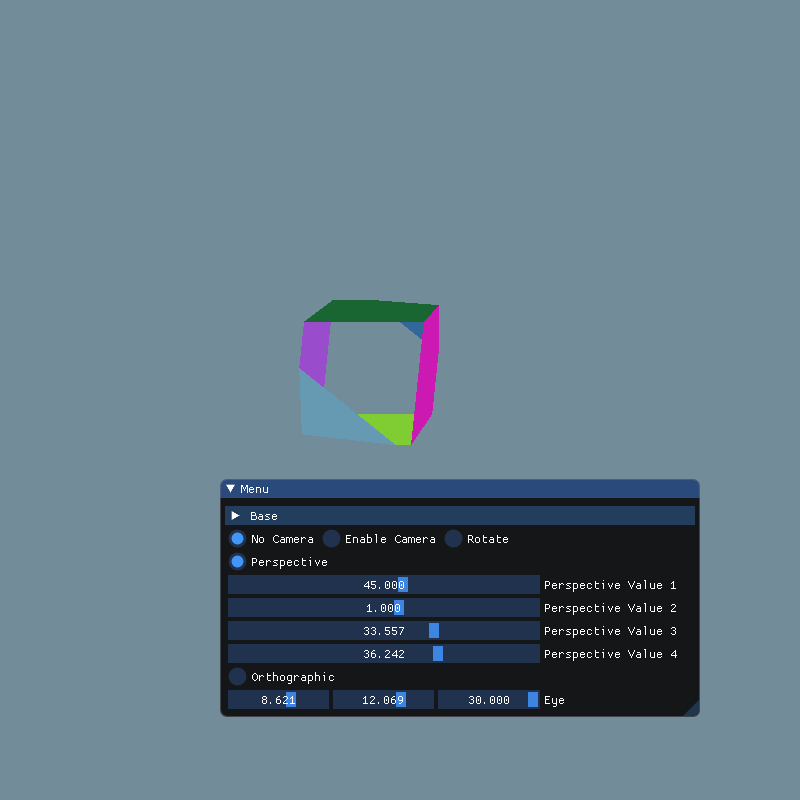
这两个参数同样可以控制 z 轴上投影的内容，上面我把他们调成刚好显示一半的正面和一半的背面

然而，当near为负数的时候，似乎实现了不太一样的效果

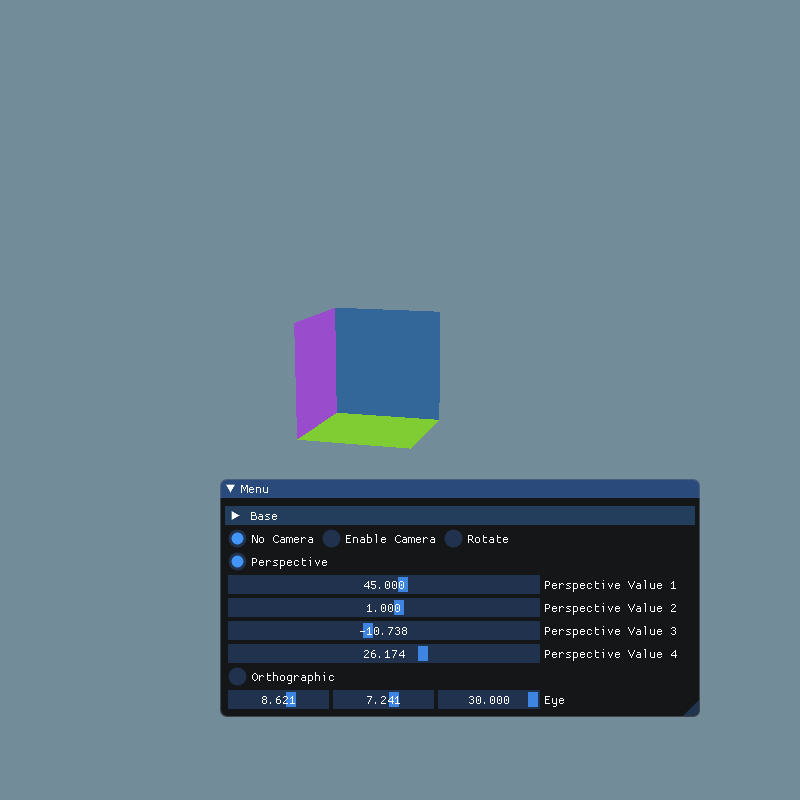
这里从网上找来了两幅图，正好可以辅助理解透视投影

投影区域	透视投影

可以看到，摄像机按一定的角度fovy和宽高比aspect向前方以锥形展开视角，然后通过变换使里面的物体映射到一个立方体视图中，然后正面说看到的内容就是透视投影后的内容，如下图所示：

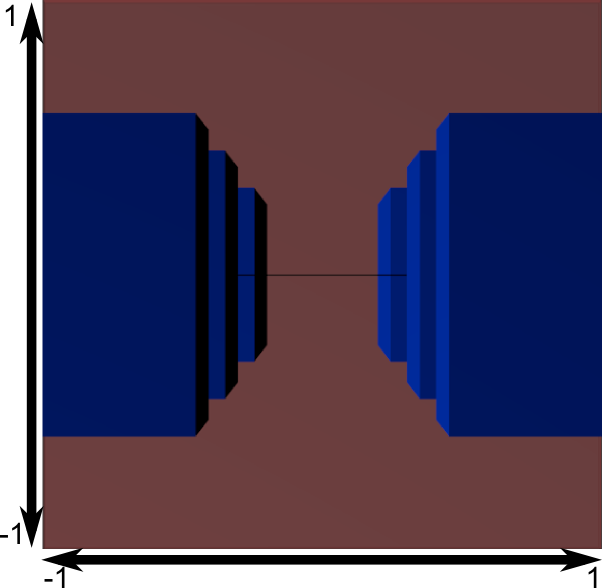
在这里，near和far就是前后两个裁剪平面，因此，如果近平面为负数的时候，就有可能处于摄像机的后面，投影后摄像机就有可能处于立方体的正中央，然后就只能显示后面的三个面了。

视角变换(View Changing)

把 cube 放置在(0, 0, 0)处，做透视投影，使摄像机围绕 cube 旋转，并且时刻看着 cube 中心

camPosX=sin(clock()/1000.0)*Radius;
camPosZ=cos(clock()/1000.0)*Radius;

原理很容易理解，由于圆的公式 a^2+b^2=1 ，以及有 sin(x)^2+cos(x)^2=1 ，所以能保证摄像机在 XoZ 平面的 一个圆上。

view = camera.GetCenterViewMatrix();
this->perspectiveValue[0] = camera.Zoom;
float clock = glfwGetTime();
float camPosX = sin(clock / 1.0) * 15.0f;
float camPosZ = cos(clock / 1.0) * 15.0f;
this->camera.Position = glm::vec3(camPosX, 5.0f, camPosZ);
this->camera.Front = glm::vec3(0.0f, 0.0f, 0.0f);
this->camera.Yaw = -90.0f;
this->camera.Pitch = 0.0f;
this->camera.Up = glm::vec3(0.0f, 1.0f, 0.0f);

这里实现了一个 Camera 类(后文再详细介绍)，使用上面的公式，让摄像机始终绕着中心点旋转，就可以得到以下的结果：

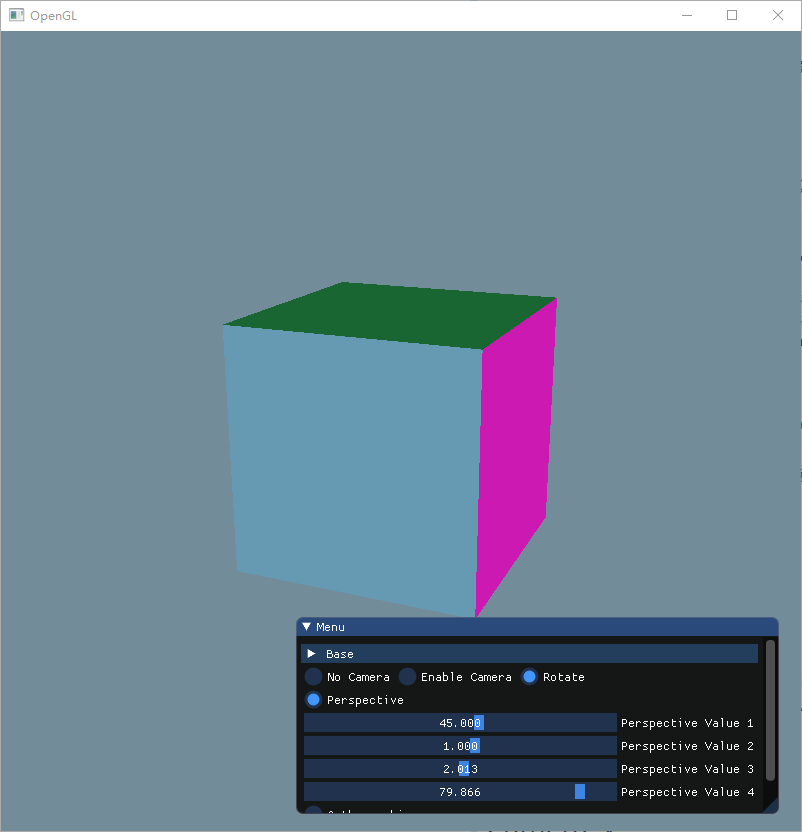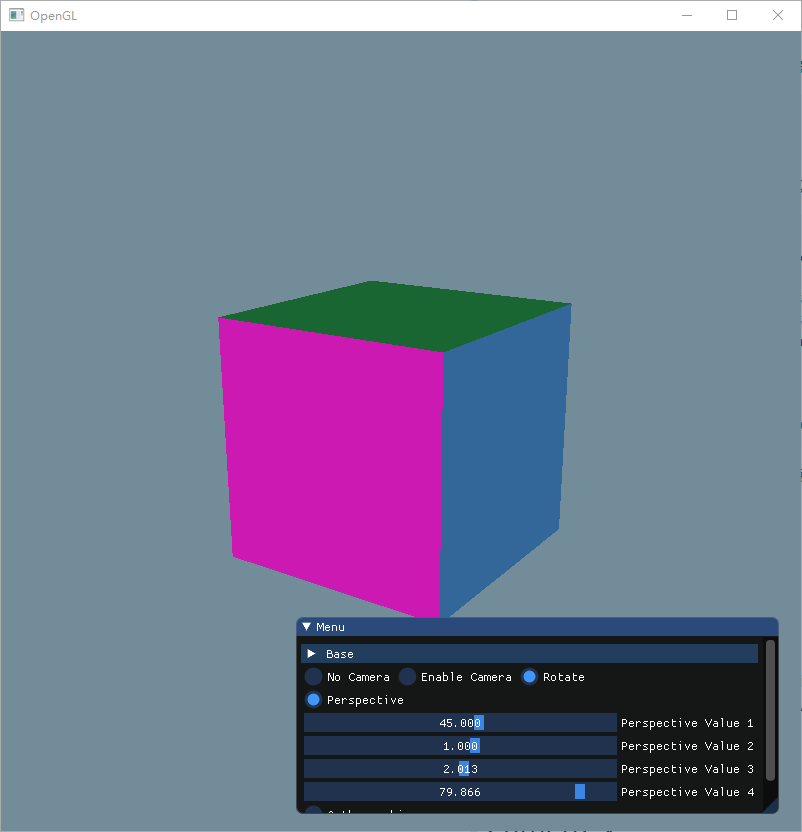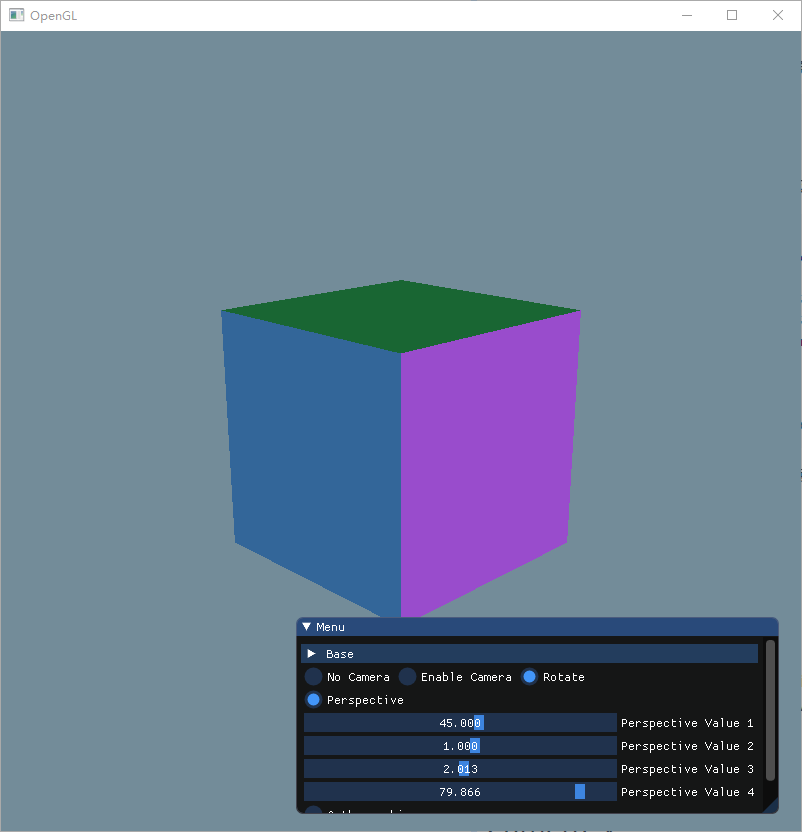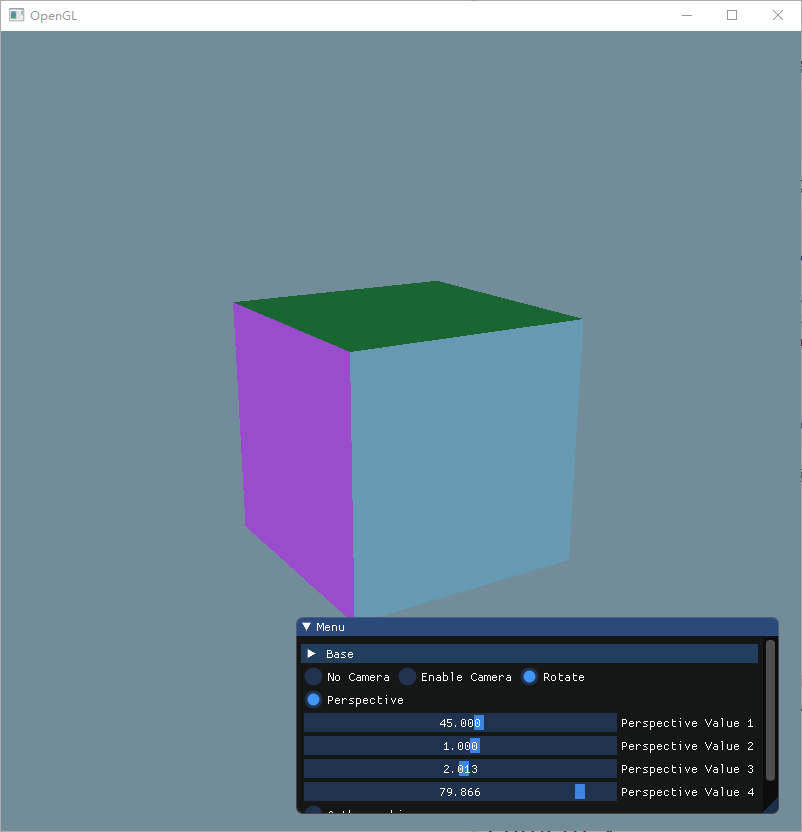
Camera 类

实现一个 camera 类，当键盘输入 w,a,s,d ，能够前后左右移动；当移动鼠标，能够视角移动(“look around”)， 即类似 FPS(First Person Shooting)的游戏场景

首先，定义一个 Camera 类

class Camera {
public:
  // Camera 属性
  glm::vec3 Position;
  glm::vec3 Front;
  glm::vec3 Up;
  glm::vec3 Right;
  glm::vec3 WorldUp;
  // Euler 角度
  float Yaw;
  float Pitch;
  // 移动灵敏度
  float MovementSpeed;
  // 鼠标灵敏度
  float MouseSensitivity;
  // 滚轮缩放
  float Zoom;
  // 是否开启控制
  bool enableControl;

  // 初始化并绑定窗口控制
  Camera(GLFWwindow* window, int height, int width);
  // 获取自由视图矩阵
  glm::mat4 GetViewMatrix();
  // 获取中心视图矩阵
  glm::mat4 GetCenterViewMatrix();
  // 更新速度
  void UpDateDeltaTime();
  // 处理键盘输入
  void ProcessInput(GLFWwindow* window);
  // 处理鼠标移动
  static void MouseCallback(GLFWwindow* window, double xpos, double ypos);
  // 处理滚轮滚动
  static void ScrollCallback(GLFWwindow* window, double xoffset, double yoffset);

private:
  // 当前状态
  float lastX;
  float lastY;
  bool firstMouse = true;
  float deltaTime = 0.0f;
  float lastFrame = 0.0f;
};

为了更好地隐藏 Camera 的细节，我把控制的绑定都集成在这个类里面，外部只需要传入window即可使用enableControl来控制摄像机是否开启控制。

首先，需要初始化数据

static Camera* CameraInst;

Camera::Camera(GLFWwindow* window, int height, int width) {
  CameraInst = this;

  this->Position = glm::vec3(0.0f, 5.0f, 20.0f);
  this->Front = glm::vec3(0.0f, 0.0f, 0.0f);
  this->WorldUp = glm::vec3(0.0f, 1.0f, 0.0f);
  this->Up = glm::vec3(0.0f, 1.0f, 0.0f);
  this->Yaw = YAW;
  this->Pitch = PITCH;
  this->MovementSpeed = SPEED;
  this->MouseSensitivity = SENSITIVITY;
  this->Zoom = ZOOM;
  this->enableControl = false;
  this->lastX = width / 2.0f;
  this->lastY = height / 2.0f;

  glfwSetCursorPosCallback(window, this->MouseCallback);
  glfwSetScrollCallback(window, this->ScrollCallback);
}

然后，通过这个类可以获取两种视图矩阵

glm::mat4 Camera::GetViewMatrix() {
  return glm::lookAt(Position, Position + Front, Up);
}

glm::mat4 Camera::GetCenterViewMatrix() {
  return glm::lookAt(Position, Front, Up);
}

前者是自由视角矩阵，即可以控制摄像机自由移动，而后者是指定一个位置，用于前面的围绕矩形旋转的实现。

然后通过计算每一帧的时间来控制移动的速度，通过WSAD控制摄像机的Position的更新，然后数字1和2设置是否捕获鼠标

void Camera::UpDateDeltaTime() {
  float currentFrame = glfwGetTime();
  deltaTime = currentFrame - lastFrame;
  lastFrame = currentFrame;
}

void Camera::ProcessInput(GLFWwindow* window) {
  float velocity = MovementSpeed * deltaTime;

  if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
    Position += Front * velocity;
  if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
    Position -= Front * velocity;
  if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
    Position -= Right * velocity;
  if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
    Position += Right * velocity;

  if (glfwGetKey(window, GLFW_KEY_1) == GLFW_PRESS)
    glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_NORMAL);

  if (glfwGetKey(window, GLFW_KEY_2) == GLFW_PRESS)
    glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);
}

对于滚轮和鼠标的移动就较为复杂。

对于鼠标的移动，我们需要记录上一次的鼠标位置，然后算出这次与上一次的偏移offset，然后把x轴的偏移加到Yaw上，把y轴的偏移加到Pitch上。更新之后，需要再次更新摄像机的Front, Right和Up数据，使用glm::cross利用方向的叉乘来实现摄像机方向的移动

void Camera::MouseCallback(GLFWwindow* window, double xpos, double ypos)
{
  if (!CameraInst->enableControl) return;
  if (CameraInst->firstMouse)
  {
    CameraInst->lastX = xpos;
    CameraInst->lastY = ypos;
    CameraInst->firstMouse = false;
  }

  float xoffset = xpos - CameraInst->lastX;
  float yoffset = CameraInst->lastY - ypos;

  CameraInst->lastX = xpos;
  CameraInst->lastY = ypos;

  xoffset *= CameraInst->MouseSensitivity;
  yoffset *= CameraInst->MouseSensitivity;

  CameraInst->Yaw += xoffset;
  CameraInst->Pitch += yoffset;

  if (CameraInst->Pitch > 89.0f)
    CameraInst->Pitch = 89.0f;
  if (CameraInst->Pitch < -89.0f)
    CameraInst->Pitch = -89.0f;

  glm::vec3 front;
  front.x = cos(glm::radians(CameraInst->Yaw)) * cos(glm::radians(CameraInst->Pitch));
  front.y = sin(glm::radians(CameraInst->Pitch));
  front.z = sin(glm::radians(CameraInst->Yaw)) * cos(glm::radians(CameraInst->Pitch));
  CameraInst->Front = glm::normalize(front);
  CameraInst->Right = glm::normalize(glm::cross(CameraInst->Front, CameraInst->WorldUp));
  CameraInst->Up = glm::normalize(glm::cross(CameraInst->Right, CameraInst->Front));
}

对于滚轮，只需改变Zoom参数，然后再使透视投影的第一个参数fovy为glm::radians(Zoom)即可实现缩放效果。

void Camera::updateCamera() {
  glm::vec3 front;
  front.x = cos(glm::radians(Yaw)) * cos(glm::radians(Pitch));
  front.y = sin(glm::radians(Pitch));
  front.z = sin(glm::radians(Yaw)) * cos(glm::radians(Pitch));
  Front = glm::normalize(front);
  Right = glm::normalize(glm::cross(Front, WorldUp));
  Up = glm::normalize(glm::cross(Right, Front));
}

最后的结果如下：