⚔ LeetCode | 218. the Skyline Problem

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

Problem

LeetCode 218. The Skyline Problem

Difficulty : Hard

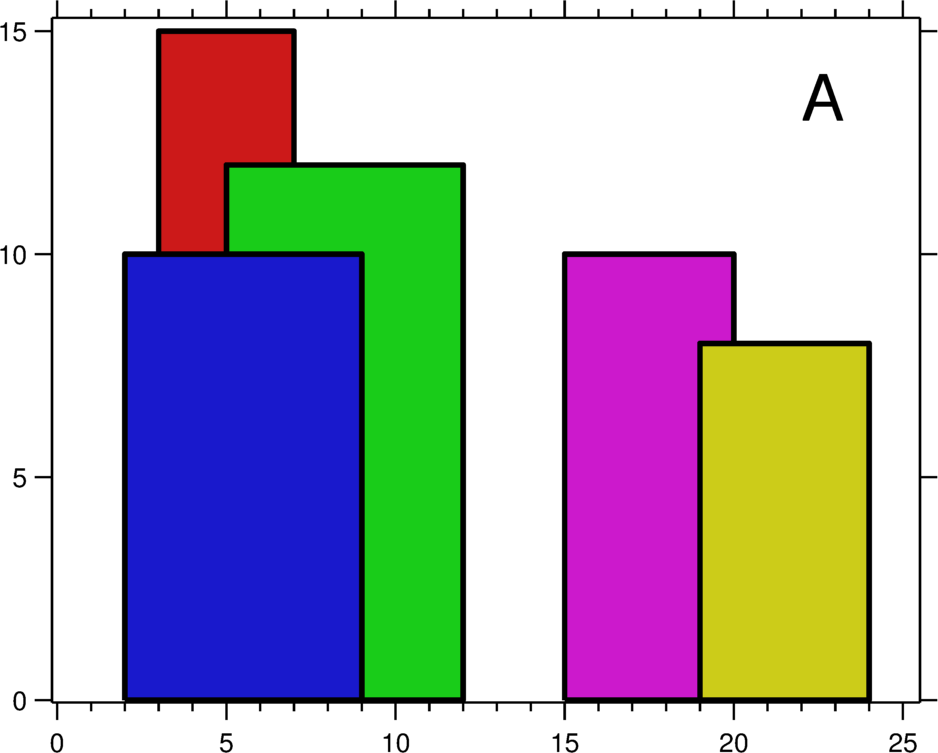
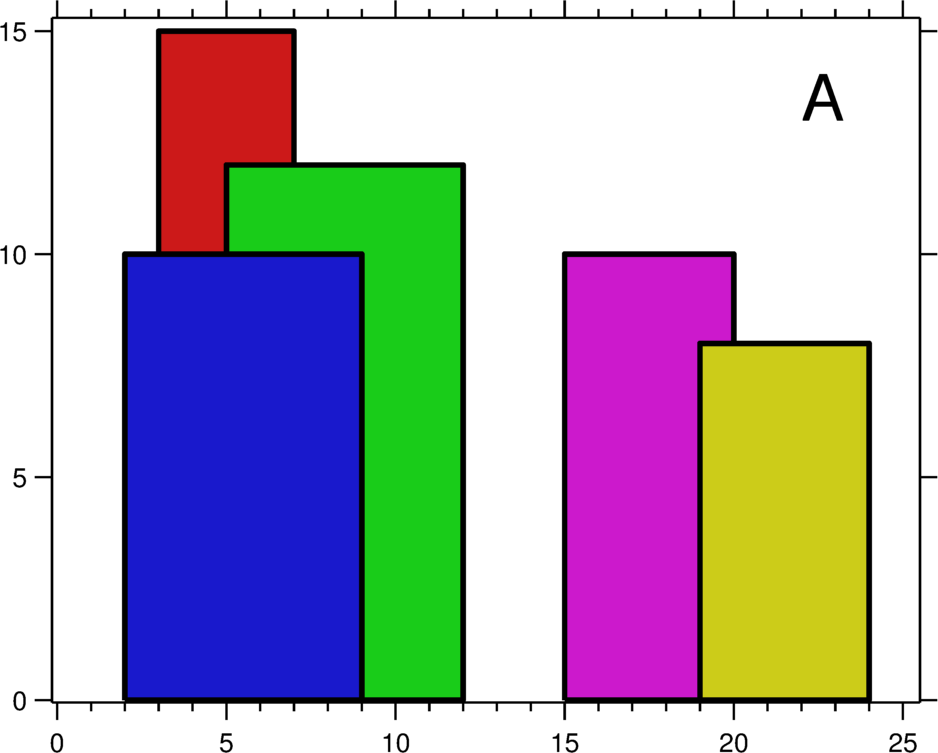
A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).

Buildings

Skyline Contour

The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ].

The output is a list of “key points“ (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.

For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].

Notes:

  • The number of buildings in any input list is guaranteed to be in the range [0, 10000].
  • The input list is already sorted in ascending order by the left x position Li.
  • The output list must be sorted by the x position.
  • There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...[2 3], [4 5], [7 5], [11 5], [12 7]...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...[2 3], [4 5], [12 7], ...]

Analysis

这道题看上去很简单，只需要找出各个矩形的边界就可以了，但实际上有很多东西都需要处理，并且如果想要达到一个比较优的复杂度还是有点难度的。

Approach 1

首先给出来的数据是一个矩形的左边界、右边界以及高度，并且是按照左边界排序的。

首先，我们先来梳理一下如何从矩形中获取这些点。

从题目的图中可以得知，左边界的点都是取最大值，而右边界的点都是取其第二大的值。

而题目给出来的数据是按左边界排序的，因此找出左边界的点是比较简单的，难点就在于如何获取右边界的点。

我们需要在当前的右边界的点从高到低处理节点，因此这里使用了优先列表这个数据结构来处理右边界的点。

具体过程如下：

  • 从左边的最左的边界开始处理，把第一个矩形的右边界和高度放入优先列表中，以高度为优先级进行排序。
  • 加入第一个左边界到结果列表中
  • 然后根据下一个矩形的左边界和最高的右边界顺序，按顺序对其进行处理
    • 对于左边界，如果当前高度是最高高度的就加入到结果当中
    • 对于右边界，弹出队列中比起低并且所有在其左边的右边界（这些边界将会被抛弃，因为并不是边界节点），然后把队列顶端高度加入到结果当中
  • 一直循环处理直到结束

对于题目的例子，我们按照这个算法来分析一下

Buildings

  • 处理蓝色方块的左边界，把点[2, 10]加入结果当中，并且把蓝色的右边界[10,9]加入优先队列中
  • 红色方块的左边界3比最高的右边界9的位置要前，因此处理红色方块的左边界，把[3,15]加入结果中，并且把[15, 7]加入优先队列
  • 绿色方块的左边界5比最高的右边界红色的7要前，处理绿色方块的左边界，但是由于其最高高度并没有发生变化，因此这条边并不是外界的边，忽略到这条边
  • 紫色方块的左边界15后于最高右边界红色的7，处理最高右边界，把在红色前面的右边界（并没有）以及自己移出队列，将当前位置和最高高度[7,12]加入结果
  • 紫色方块的左边界15还是后于最高右边界绿色的12，因此把在绿色前面的右边界（蓝色）和自己移出队列，将当前位置和最高高度[12,0]加入结果
  • 当前队列没有最高右边界了，因此直接将紫色的左边界点[15,10]加入结果，并且把右边界[10,20]加入优先队列中
  • 黄色方块的左边界16比最高的右边界紫色的20要前，处理黄色方块的左边界，但是由于其最高高度并没有发生变化，因此这条边并不是外界的边，忽略到这条边。并且把黄色的右边界[24,8]加入优先队列中
  • 当前没有左边界了，从高到低依次处理右边界，最高右边界为紫色的20，把在紫色前面的右边界（并没有）以及自己移出队列，将当前位置和最高高度[20,8]加入结果
  • 当前没有左边界了，从高到低依次处理右边界，最高右边界为黄色的的40，把在黄色前面的右边界（并没有）以及自己移出队列，将当前位置和最高高度[24,0]加入结果

最后得出题目的结果：

[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]

C++代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
  vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {
    vector<pair<int, int>> res;
    priority_queue <pair<int,int>> rightHeight; // 存储高度和右边界（按高度从小到大排序）
    int current = 0, x = 0,  height = -1, len = buildings.size();
    while (current < len || !rightHeight.empty()) {
      x = rightHeight.empty() ? buildings[current][0] : rightHeight.top().second;
      if (current >= len || buildings[current][0] > x) {
        // 弹出已处理完的矩形
        while (!rightHeight.empty() && rightHeight.top().second <= x) rightHeight.pop();
      } else {
        x = buildings[current][0];
        while (current < len && buildings[current][0] == x) {
          rightHeight.push(make_pair(buildings[current][2], buildings[current][1]));
          current++;
        }
      }
      height = rightHeight.empty() ? 0 : rightHeight.top().first;
      if (res.empty() || res.back().second != height) res.push_back(make_pair(x, height));
    }
    return res;
  }
};

这个算法需要遍历一次各个数组处理左边界，在此同时还需要处理右边界。总的来说平均每一个矩形的左边界和右边界都会经过一次处理，因此时间复杂度大概是O(2n)，也就是O(n)

Summary

这道题处理起来的逻辑是有一点复杂，需要思路十分清晰才能编写出没有错误的代码，并且需要借助优先队列对其右边界进行有优先级的处理。优先队列对其时间复杂度的优化具有很大的作用，没有优先队列的话需要一个循环中需要多次遍历右边界队列。

土豪通道
0%