⚔ LeetCode | 51. N-Queens

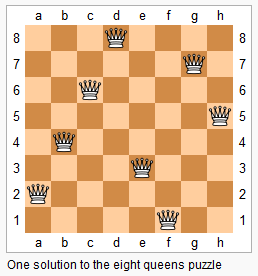
Problem

LeetCode 51. N-Queens

Difficulty : Hard

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Example:

Input: 4
Output: [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

Analysis

这是一道传统的 N 皇后问题，那就使用传统的递归方式来解决他。

Approach 1

在一般的 N 皇后问题里面，我们一般需要大量的循环来判断当前列，左斜对角，右斜对角是否已经存在了皇后。

这里我使用空间换取时间的方法，使用布尔数组来代表当前列，左斜对角，右斜对角是否已经存在了皇后

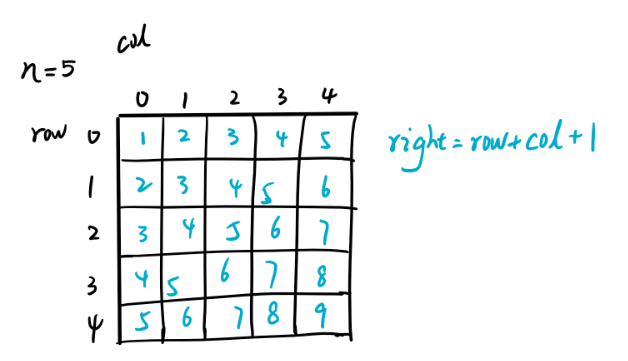
定义三个布尔数组col, left, right ，其大小分别为n, 2n,2n

使用 DFS 对于每一行r遍历所有的列c，如果

• col[c] == false
• left[n - r + c] == false
• right[r + c + 1] == false

那么当前列，左斜对角，右斜对角并不存在皇后，因此可以把新的皇后放到这个位置，同时将上面三个布尔变量设置为true，直到回溯回来进行下一列的时候把他们设置为false

对于列的判断很好理解，对于左斜对角和右斜对角的判断可以看下图：

左斜对角：

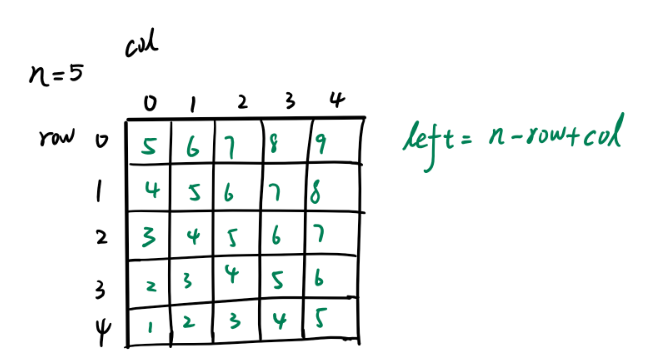
右斜对角：

这样，就可以使用O(1)的复杂度来判断当前位置是否可以放下一个新的皇后了。

Golang的代码如下：

func solveNQueens(n int) [][]string {
	row := make([]int, n)
	col := make([]bool, n)
	left := make([]bool, 2*n)
	right := make([]bool, 2*n)
	res :=  make([][]string, 0)
	findNQueens(n,0 ,&row, &col, &left, &right, &res)
	return res
}

func findNQueens(n, r int, row *[]int, col, left, right *[]bool, res *[][]string) {
	if r == n {
		var solve []string
		blankRow := make([]byte, n)
		for j := 0; j < n; j++ {
			blankRow[j] = '.'
		}
		for i := range *row {
			newRow := make([]byte, n)
			copy(newRow, blankRow)
			newRow[(*row)[i]] = 'Q'
			solve = append(solve, string(newRow))
		}
		*res = append(*res, solve)
		return
	}
	for c := 0; c < n; c++ {
		if (*col)[c] == false && (*left)[n - r + c] == false && (*right)[c + r + 1] == false{
			(*row)[r] = c
			(*col)[c] = true
			(*left)[n - r + c] = true
			(*right)[c + r + 1] = true
			findNQueens(n, r + 1, row, col, left, right ,res)
			(*col)[c] = false
			(*left)[n - r + c] = false
			(*right)[c + r + 1] = false
		}
	}
}

这里使用回溯法求解 N 皇后问题，对于每次判断当前位置是否可以放下来，这里已经优化到O(1)的程度，因此这段代码在LeetCode上只花费了8ms，快于所有的Golang提交。

Runtime: 8 ms, faster than 100.00% of Go online submissions for N-Queens.

Summary

这道题是很传统的算法题，使用了回溯法。虽然也是一道Hard题，但是如果熟悉回溯法的话还是很容易就可以解决的。