⚔ LeetCode | 85. Maximal Rectangle

Problem

Difficulty : Hard

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.

Example :

Input:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
Output: 6

Analysis

上个星期来在直方图里面找最大的矩形，这个星期就继续下一道hard题：从矩阵中寻找最大的矩形。

看上去需要一些动态规划的方法

Approach 1

老规矩，从最简单最暴力的方法入手，找到最基本的思路先。

对于矩阵里面的每一个元素，如果元素是1，我们可以寻找出以这个点为左上角的最大的矩形。

然后取其最大值就是矩阵中最大的矩形。

具体的做法如下：

对于矩阵中的每一个元素：

首先向右扩展，找到第一个非1的位置，作为矩形的有边界，然后就形成一个矩形（高度为1），计算出矩形的面积，记录到max中
然后向下扩展，重新从当前列向右扩展，找到第一个非全1的位置，记录为矩形的右边界，然后形成一个新的矩形（高度为2），计算出矩形面积，与max比较，并留下最大值。
直到遇到当前列第一个非1元素就可以停止下来

这样，我们就可以得到以这个点为左上角的最大的矩形，绝对不会漏掉一个。

只是这种做法实在是太暴力了 👊。

代码如下：


func maximalRectangle2(matrix [][]byte) int {
	max := 0
	for i := range matrix {
		for j := range matrix[i] {
			if matrix[i][j] == '1' {
				nextI := i
				for nextI < len(matrix) {
					nextJ := j + 1
					for nextJ  < len(matrix[i]) {
						amdYes := true
						for k := i; k <= nextI; k++ {
							if matrix[k][nextJ] != '1' {
								amdYes = false
								break
							}
						}
						if amdYes == false {
							break
						}
						nextJ++
					}
					area := (nextJ - j) * (nextI - i + 1)
					if area > max {
						max = area
					}
					if nextI + 1 < len(matrix) &&
						matrix[nextI + 1][j] == '1' {
						nextI++
					} else {
						break
					}
				}
			}
		}
	}
	return max
}

这种做法对于每一个元素最坏情况下都要遍历一次右边的所有元素，因此其时间复杂度为$O(n^2)$，在所有提交中只打败了20%的提交，耗时 20 ms，因此，这个算法有很大的提升空间。

Approach2

这时候需要用到一些动态规划的技巧了。

主要思路还是和上面差不多，但是我们可以减少一些不必要的操作。

基本思想是使用数组记录当前的最大矩形的边界，然后使得下一次的计算可以使用上一次的结果，这样就可以节省大量的计算量

具体的做法如下：

定义长度为矩阵列数的数组left, right, height
将left,height初始化为0, right初始化为矩阵列数
对矩阵的每一行进行遍历：
- 对于这一行的每一个元素i：
  - 如果第i个元素是1，那么height[i]++否则height[i] = 0。（这样就可以判断出当前列的最高高度，而且对于下一行的判断也可以基于之前的数值，减少了需要遍历的元素数量）
  - 定义当前的左边界和右边界为curLeft, curRight
  - 从左到右遍历当前行
    - 如果当前元素为1，那么left[i]取left[i]和curLeft的最大值（这样就可以判断出当前高度的最左边界，确保矩形范围内的元素都为1）
    - 如果当前元素为0，那么清空left[i]，设置为0，重新设置curLeft为i + 1
  - 同样，从右到左遍历当前行，设置right中的右边界
    - 如果当前元素为1，那么right[i]取它和curRight中的最小值
    - 如果当前元素为0，那么将right[i]设置为矩阵的列数，curRight也设置为i
最后，我们得到以每一列中的最大的矩形的左边界，右边界以及高度，根据这个数据就可以算出其代表的矩阵的面积大小
最后取其最大值返回

这里有两张图片可以辅助理解：

006tNbRwly1fvx7px08o3j311o1tvtkv

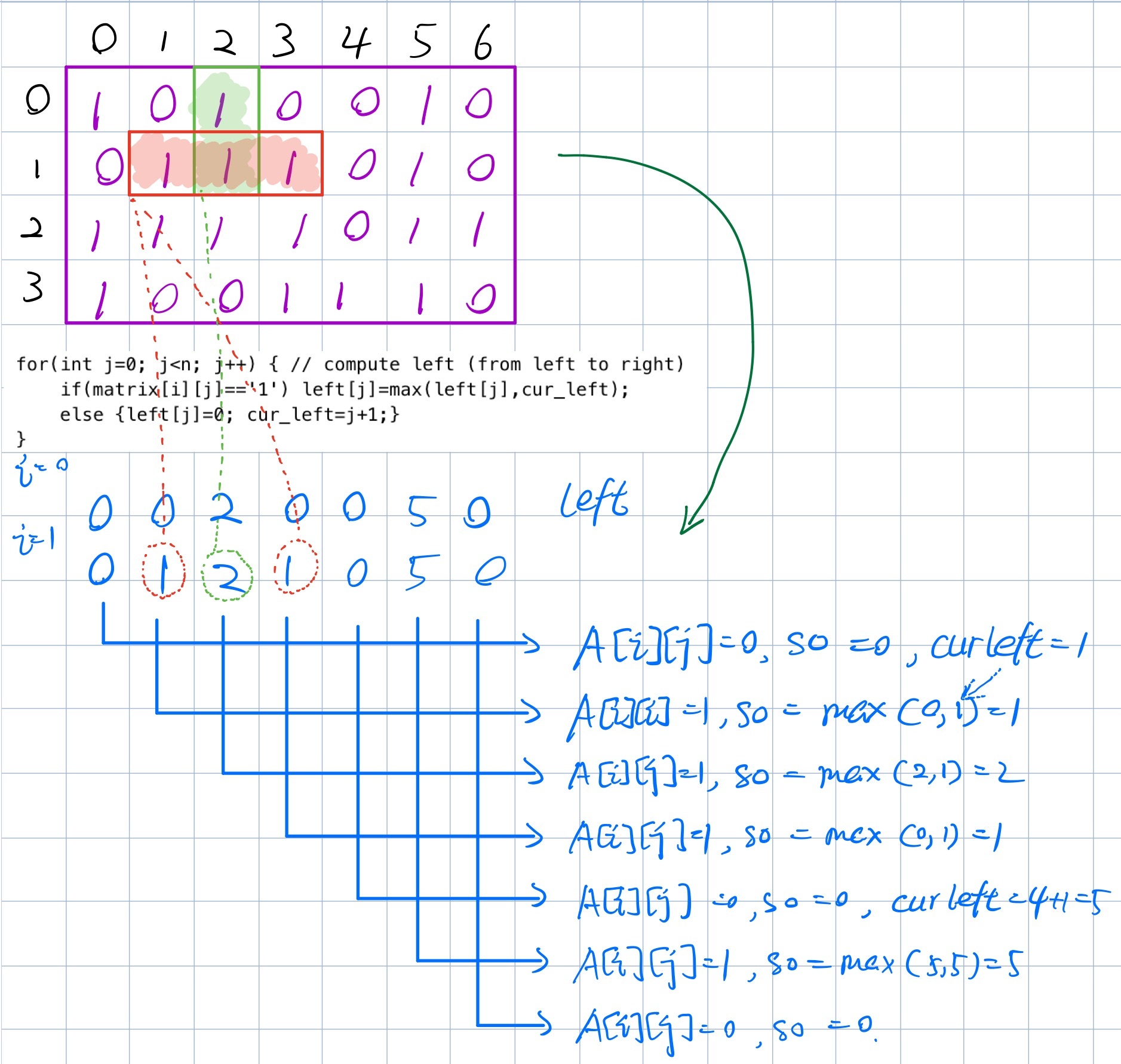
006tNbRwly1fvx8ckb539j31g51digzi

证明

为什么这个算法可以找出最大的矩阵呢？

原因很简单，这个算法找出来的矩阵是以每一列的最大高度作为基准，向左右两边做出最大的扩展。如果存在一个矩形，那么肯定最先找到他一条垂直的边，上面和下面的元素都为0，如果不存在这个边，那么证明这个矩形并不是最大的面积，他还可以向上或者向下扩展。

代码如下：


func maximalRectangle(matrix [][]byte) int {
	if len(matrix) == 0 {
		return 0
	}
	rows, cols := len(matrix), len(matrix[0])
	left, right, height := make([]int, cols), make([]int, cols), make([]int, cols)
	max := 0
	for i := 0; i < cols; i++ {
		right[i] = cols
	}
	for i := 0; i < rows; i++ {
		curLeft, curRight := 0, cols
		for j := 0; j < cols; j++ {
			if matrix[i][j] == '1' {
				height[j]++
				if left[j] < curLeft {
					left[j] = curLeft
				}
			} else {
				height[j] = 0
				left[j] = 0
				curLeft = j + 1
			}
		}
		for j := cols - 1; j >= 0; j-- {
			if matrix[i][j] == '1' {
				if right[j] > curRight {
					right[j] = curRight
				}
			} else {
				right[j] = cols
				curRight = j
			}
		}
		for j := 0; j < cols; j ++ {
			area := (right[j] - left[j]) * height[j]
			if area > max {
				max = area
			}
		}
	}
	return max
}