⚔ LeetCode | 84. Largest Rectangle in Histogram

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

Problem

LeetCode 84. Largest Rectangle in Histogram

Difficulty : Hard

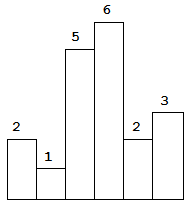
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

img
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

img
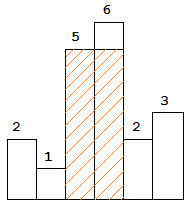
The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example :

1
2
Input: [2,1,5,6,2,3]
Output: 10

Analysis

这道题的题意是要求我们在一个给定的直方图中寻找最大的矩形。

Approach 1

首先， 从最简单最暴力的方法入手。

对于每一个元素，我们都可以找出一个以当前元素为高度的最大的矩形，那么，只需要遍历所有元素，就可以找出面积最大的矩形。

具体的做法如下：

对于数组中的每一个元素:

  • 找出其左边第一个小于自身的元素的位置l
  • 找出其右边第一个小于自身的元素的位置r
  • 当前元素的高度h * (r - l - 1)就是以当前元素为高度的最大的矩形

然后找出所有元素中最大的矩形，就是本题的答案

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func largestRectangleArea(heights []int) int {
	max := 0
	for i := range heights {
		left, right := i, i
		for j := i + 1; j < len(heights); j++ {
			if heights[j] < heights[i] {
				break
			}
			right = j
		}
		for j := i - 1; j >= 0; j-- {
			if heights[j] < heights[i] {
				break
			}
			left = j
		}
		area := heights[i] * (right - left + 1)
		if area > max {
			max = area
		}
 	}
	return max
}

这种做法对于每一个元素最坏情况下都要遍历一次每一个元素，因此其时间复杂度为$O(n^2)$，在所有提交中只打败了12.5%的提交，耗时 960 ms，因此，这个算法有很大的提升空间

Approach2

我们可以使用一些技巧，将前面查询的左边界和右边界存储下来。

使用两个数组LeftLess和RightLess,用于存储当前位置上的左边界和右边界，用空间换取时间

具体做法如下：

  • 为LeftLess的第一个元素赋值-1，表示左边的尽头

  • 为RightLess的最后一个元素赋值数组的长度，表示右边的尽头

  • 从左边到右边遍历数组，寻找左边界：

    • 设left为左边元素的下标
    • 如果left不是左边的尽头-1
      • left中的元素的数值大于自己的数值，那么将自己的左边界设为left元素的左边界 left = LeftLess[left]
      • 继续重复上面的步骤，直到左尽头或者遇到小于自己的数值
    • 设当前元素的左边界为left

  • 从右边到左边遍历数组，寻找右边界：

    • 设left为左边元素的下标
    • 如果left不是左边的尽头-1
      • right中的元素的数值大于自己的数值，那么将自己的左边界设为right元素的左边界 right = RightLess[right]
      • 继续重复上面的步骤，直到左尽头或者遇到小于自己的数值
    • 设当前元素的左边界为right

这种做法利用了之前元素的边界值来判断当前元素的边界值，比上面那种做法少了不少操作。

最后根据元素的高度和左右边界，就可以计算出以当前元素为高度的最大的矩形的面积

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func largestRectangleArea(heights []int) int {
	l := len(heights)
	if l < 1 {
		return 0
	}
	leftLess := make([]int, l)
	rightLess := make([]int, l)
	leftLess[0] = -1
	rightLess[l - 1] = l
	for i := 1; i < l; i++ {
		left := i - 1
		for left >= 0 && heights[left] >= heights[i] {
			left = leftLess[left]
		}
		leftLess[i] = left
	}
	for i := l - 2; i >= 0; i-- {
		right := i + 1
		for right < l && heights[right] >= heights[i] {
			right = rightLess[right]
		}
		rightLess[i] = right
	}
	max := 0
	for i := 0; i < l; i++ {
		area := heights[i] * (rightLess[i] - leftLess[i] - 1)
		if area > max {
			max = area
		}
	}
	return max
}

由于基本上只需要很少的操作就可以判断出当前元素的边界值，因此其时间复杂度可以近似看作$O(n)$，这个提交在LeetCode上超过了100%的提交，只花了 12 ms，应该是go语言最优的做法。

Approach3

上面那种解法需要使用两个数组，但是其实使用一个堆栈也是可以解决的。

下面是使用堆栈的一种解决方式，其基本思想和上面有所不同，不过也是大同小异的。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func largestRectangleArea(heights []int) int {
	l := len(heights)
	max := 0
	stacks := make([]int, l + 1)
	is := -1
	for i := 0; i <= l; i++ {
		h := 0
		if i != l {
			h = heights[i]
		}
		for is != -1 && h < heights[stacks[is]] {
			hh := heights[stacks[is]]
			is--
			width := i
			if is != -1 {
				width = i - 1 - stacks[is]
			}
			if hh * width > max {
				max = hh * width
			}
		}
		is++
		stacks[is] = i
	}
	return max
}

这种算法虽然空间复杂度比上面的做法低，但是耗费的时间却比上面的做法多一点。

Summary

第二种解法和第一种解法，其核心的思想基本上没有什么区别，但是耗费的时间上却差了几乎 100 倍。这就是优化算法的必要性。一些简单的技巧可以极大地优化我们的算法。

土豪通道
0%