📝 Code | MD5算法设计与实现

上个月用Golang和Cpp实现了 DES 算法，这次用Cpp来实现一个 MD5 算法，与 DES 相比，MD5 还是算比较简单的。

🚀 代码: Github

算法原理概述

MD5 算法全称MD5 信息摘要算法(MD5 Message-Digest Algorithm)， 是一种比较常见和简单的密码散列函数，用于生成一个 128 位的散列值确保信息传输完整一致。由于 MD5 的不可逆性，一般会用来加密保存在数据库中的密码字串，又由于 MD5 存在扩散性，即使原来的数据只有 1 位错误，生成出来的散列值都会完全不同，因此也可以用于计算数据指纹。

MD5 算法的主要原理就是对原始数据经过多次的迭代，将数据中的每一位都重复混淆和扩散到散列值当中。

总体结构

其基本的算法流程如下图：

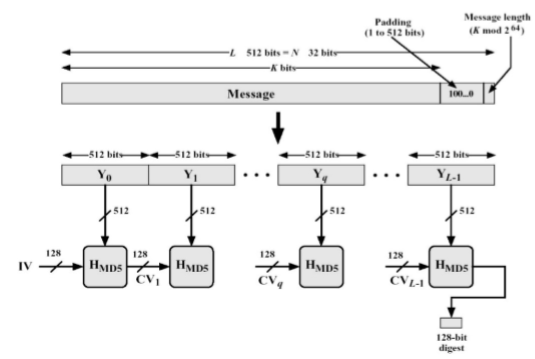
MD5 算法的基本过程为：填充、分块、缓冲区初始化、循环压缩、得出结果

将原始数据填充并划分为 512 位的块后，每一个数据块，对初始向量(IV)使用四个不同的生成函数进行 4 轮循环迭代，在每次循环中结合 T 表元素和 512 位的原始数据进行 16 次迭代，将数据充分扩散和混淆。

最后将初始向量经过迭代之后的值以 16 进制输出，就是 MD5 算法生成的散列值。

模块分解

我们可以将 MD5 算法分为填充分块和循环压缩两个基本模块

填充分块

首先是填充和分块

在加密压缩之前，我们先要保证数据是 512 位的整数倍，也就是说需要划分若干个为 512 位的数据块，如果一个数据块不够 512 位，就必须填充够 512 位。

由于消息的尾部还需要附加原始信息位数的低 64 位，因此需要保证最后一块的位数为512-64=488位。

由于这里用字符串作为原始消息，因此每一位字符是占 8 位（1Byte）的，因此每一个块就为64Byte，填充是使用1000......000来补全剩余的字符的，因此第一位填充0x80，后面填充0x00

首先计算需要填充的0x00的个数

int paddingCount = len % 64;
paddingCount = paddingCount > 55 ? 119 - paddingCount
                                   : 55 - paddingCount;  // 填充0x0的个数

如果目前最后一块的字节小于56，那只需要填充满这一块的前56位

如果目前最后一块的字节大于或等于56，就需要额外填充一块，使得直到填充满下一块的前56位

// 读取数据
for (int i = 0; i < len; i++) {
  bitset.AddByte(data[i]);
}
// 填充首位1
bitset.AddByte(0x80);
// 填充0
for (int i = 0; i < paddingCount; i++) {
  bitset.AddByte(0x00);
}

最后把原始信息位数的低 64 位填充到最后一块，使得其长度达到512位

vector<bit32> parts = bitset.GetBitSet();
// 填充(长度 mod 2^64)
parts.push_back((len * 8) & 0xffff);
parts.push_back(((len * 8) >> 32) & 0xffff);
MD5::parts = parts;

最后每一块得出 16 个32位的数据分块

循环压缩

MD5 算法中对于数据最主要的操作就在于循环压缩部分

首先需要对初始向量进行初始化

A= 0x67452301
B= 0xEFCDAB89
C= 0x98BADCFE
D= 0x10325476

需要注意的是，这里的初始向量在内存当中需要为小端编码保存，即将低位字节放在内存的低地址段。否则接下来进行移位的时候数据会有不同，C 和 C++都是使用小端编码的，而 Java 是采用大端编码。

对于每 512 位原始数据，进行 4*16 次迭代

在 4 轮迭代中，使用不同的函数对于上面初始化的B,C,D进行操作

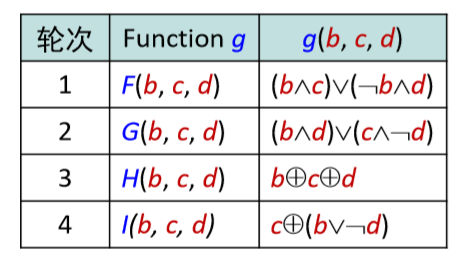
然后在 4 次迭代中，进行 16 次迭代

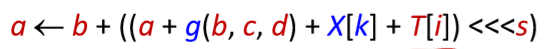
其中

• g 为上面的函数

• X 为本轮 16 个 32 位的分块的第k个 32 位分块

  • K 在每一轮中分别由不同的方法确定，这里将其生成为一个 64 个元素的表，根据当前迭代次数获取

• T 同样为一个表，是由指定函数生成的$T[i] = int(2^{32}\times|sin(i)|)$，为了计算速度，这里同样生成一个 64 个元素的表，根据迭代次数获取

• s 为循环左移，同样是预设的一个 64 个元素的表

经过 64 次迭代之后，将 ABCD 向右循环移动一个位置

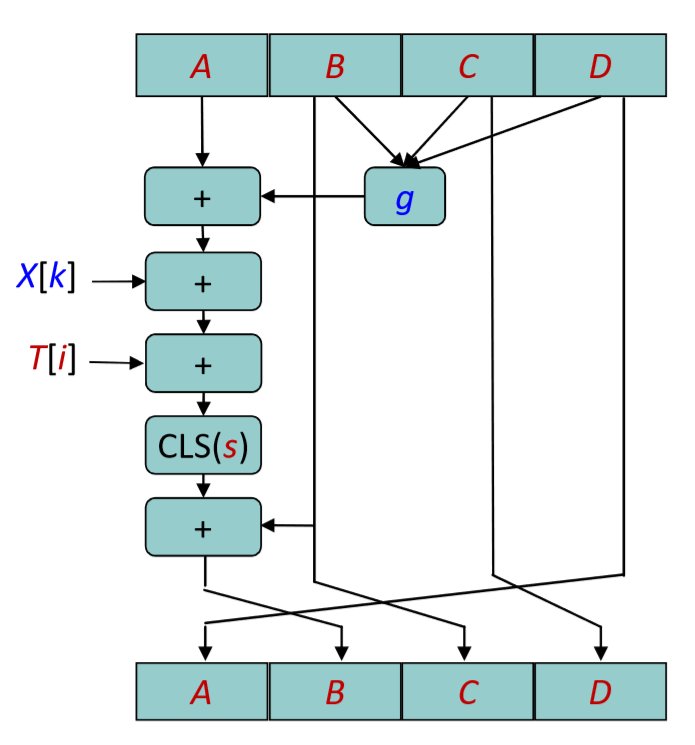
对消息中的每 512 位做上面的迭代处理。

最后将 128 位的 ABCD 以 16 进制输出，就可以得到 32 位的 16 进制散列值字符串

注意：需要以小端模式输出

数据结构

首先定义上面的各种表

namespace MD5 {
// MD缓冲区 （初始化为初始向量）
bit32 MD[4] = {0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476};
// T表
bit32 T[64] = {
    0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a,
    0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be,
    0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340,
    0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
    0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8,
    0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c,
    0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70, 0x289b7ec6, 0xeaa127fa,
    0xd4ef3085, 0x04881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
    0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92,
    0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
    0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391};
// S表（移位位数）
byte s[64] = {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22,
             5, 9,  14, 20, 5, 9,  14, 20, 5, 9,  14, 20, 5, 9,  14, 20,
             4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23,
             6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21};
// X表（对原始消息取值的位置）
byte X[4][16] = {{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15},
                {1, 6, 11, 0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 1},
                {5, 8, 11, 14, 1, 4, 7, 10, 13, 0, 3, 6, 9, 12, 15, 2},
                {0, 7, 14, 5, 12, 3, 10, 1, 8, 15, 6, 13, 4, 11, 2, 9}};
// 存储32bit的分块
vector<bit32> parts;
};  // namespace MD5

C 语言源代码

Github

MD5.h

#ifndef MD5_H
#define MD5_H
#include <iostream>
#include <sstream>
#include <string>
#include <vector>
typedef unsigned char byte;
typedef unsigned int bit32;

std::string getMD5(const byte* data, size_t len);

#endif

MD5.cpp

#include "md5.h"

using std::cout;
using std::endl;
using std::string;
using std::vector;

namespace MD5 {
bit32 MD[4] = {0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476};
bit32 IV[4] = {0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476};
bit32 T[64] = {
    0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a,
    0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be,
    0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340,
    0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
    0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8,
    0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c,
    0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70, 0x289b7ec6, 0xeaa127fa,
    0xd4ef3085, 0x04881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
    0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92,
    0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
    0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391};
byte s[64] = {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22,
             5, 9,  14, 20, 5, 9,  14, 20, 5, 9,  14, 20, 5, 9,  14, 20,
             4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23,
             6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21};
byte X[4][16] = {{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15},
                {1, 6, 11, 0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 1},
                {5, 8, 11, 14, 1, 4, 7, 10, 13, 0, 3, 6, 9, 12, 15, 2},
                {0, 7, 14, 5, 12, 3, 10, 1, 8, 15, 6, 13, 4, 11, 2, 9}};
vector<bit32> parts;
};  // namespace MD5

class BitSet32 {
 public:
  BitSet32() {
    current = 0;
    pos = 0;
  }
  void AddByte(byte b) {
    current |= (b << (pos * 8));
    pos++;
    if (pos == 4) {
      parts.push_back(current);
      current = 0;
      pos = 0;
    }
  }
  vector<bit32> GetBitSet() { return parts; }

 private:
  vector<bit32> parts;
  bit32 current;
  int pos;
};

// 小端编码
void encode(const bit32* input, byte* output, size_t length) {
  for (size_t i = 0, j = 0; j < length; ++i, j += 4) {
    output[j] = (byte)(input[i] & 0xff);
    output[j + 1] = (byte)((input[i] >> 8) & 0xff);
    output[j + 2] = (byte)((input[i] >> 16) & 0xff);
    output[j + 3] = (byte)((input[i] >> 24) & 0xff);
  }
}

// 填充
void padding(const byte* data, size_t len) {
  int paddingCount = len % 64;
  paddingCount = paddingCount > 55 ? 119 - paddingCount
                                   : 55 - paddingCount;  // 填充0x0的个数
  BitSet32 bitset = BitSet32();
  // 读取数据
  for (int i = 0; i < len; i++) {
    bitset.AddByte(data[i]);
  }
  // 填充首位1
  bitset.AddByte(0x80);
  // 填充0
  for (int i = 0; i < paddingCount; i++) {
    bitset.AddByte(0);
  }
  vector<bit32> parts = bitset.GetBitSet();
  // 填充(长度 mod 2^64)
  parts.push_back((len * 8) & 0xffff);
  parts.push_back(((len * 8) >> 32) & 0xffff);
  MD5::parts = parts;
}

// 压缩
void H_MD5() {
  int count = MD5::parts.size() / 16;  // 循环次数
  for (int q = 0; q < count; q++) {
    bit32 ta = MD5::MD[0];
    bit32 tb = MD5::MD[1];
    bit32 tc = MD5::MD[2];
    bit32 td = MD5::MD[3];
    for (int j = 0; j < 4; j++) {
      for (int i = 0; i < 16; i++) {
        int rounds = j * 16 + i;
        bit32 a = ta;
        bit32 b = tb;
        bit32 c = tc;
        bit32 d = td;
        a += MD5::parts[q * 16 + MD5::X[j][i]] + MD5::T[rounds];
        switch (j) {
          case 0:
            a += (b & c) | (~b & d);
            break;
          case 1:
            a += (b & d) | (c & ~d);
            break;
          case 2:
            a += (b) ^ (c) ^ (d);
            break;
          case 3:
            a += c ^ (b | ~d);
            break;
        }
        a = (a << MD5::s[rounds] | a >> (32 - MD5::s[rounds])) + b;
        ta = d;
        tb = a;
        tc = b;
        td = c;
      }
    }
    MD5::MD[0] += ta;
    MD5::MD[1] += tb;
    MD5::MD[2] += tc;
    MD5::MD[3] += td;
  }
}

string getMD5(const byte* data, size_t len) {
  // 填充
  padding(data, len);
  // MD5压缩函数
  H_MD5();
  // 对结果进行小端编码
  byte digest[16];
  encode(MD5::MD, digest, 16);
  // 输出十六进制字符串
  std::ostringstream ss;
  ss << std::hex;
  for (int i = 0; i < 16; i++) {
    if (digest[i] < 16) ss << 0;
    ss << (int)digest[i];
  }
  ss << endl;
  return ss.str();
}

test.cpp

#include <iostream>
#include "md5.h"
using namespace std;

int main(int argc, char const* argv[]) {
  string in;
  cin >> in;
  const unsigned char* data = (const unsigned char*)in.c_str();
  cout << getMD5(data, in.length());
  return 0;
}

编译运行结果

首先对一个短的字符串测试

然后在网上找一个MD5 生成的工具进行比对测试

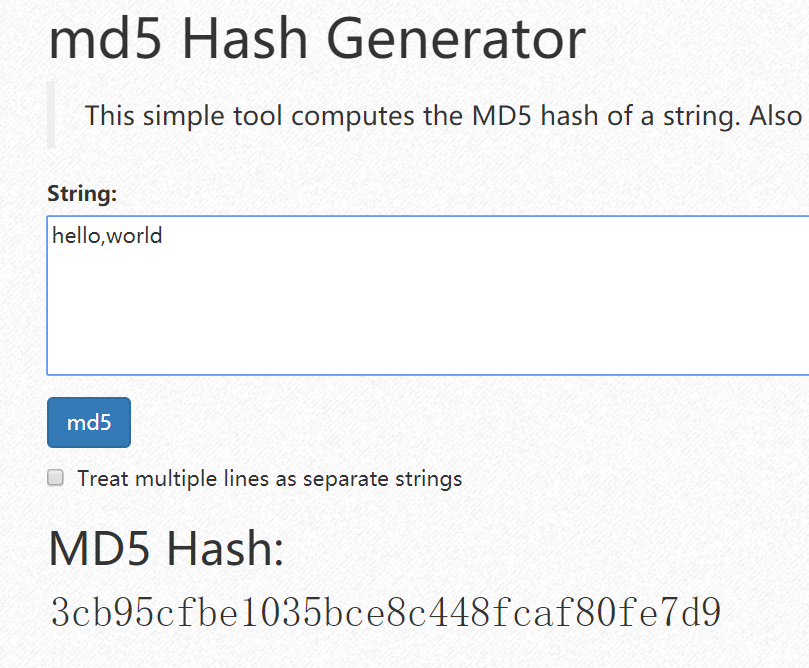
生成的结果是一致的

然后对一个比较长的字符串测试

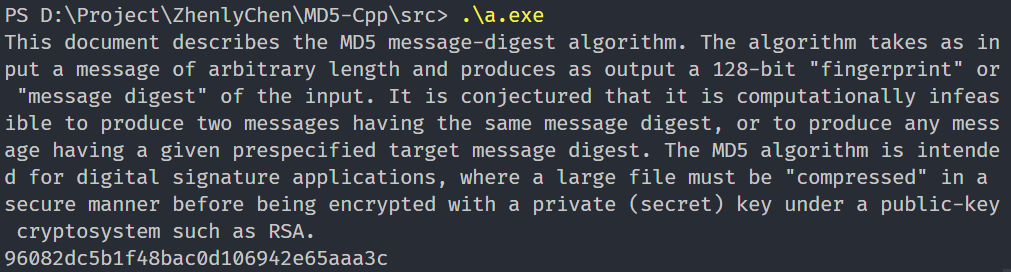
其他工具生成结果

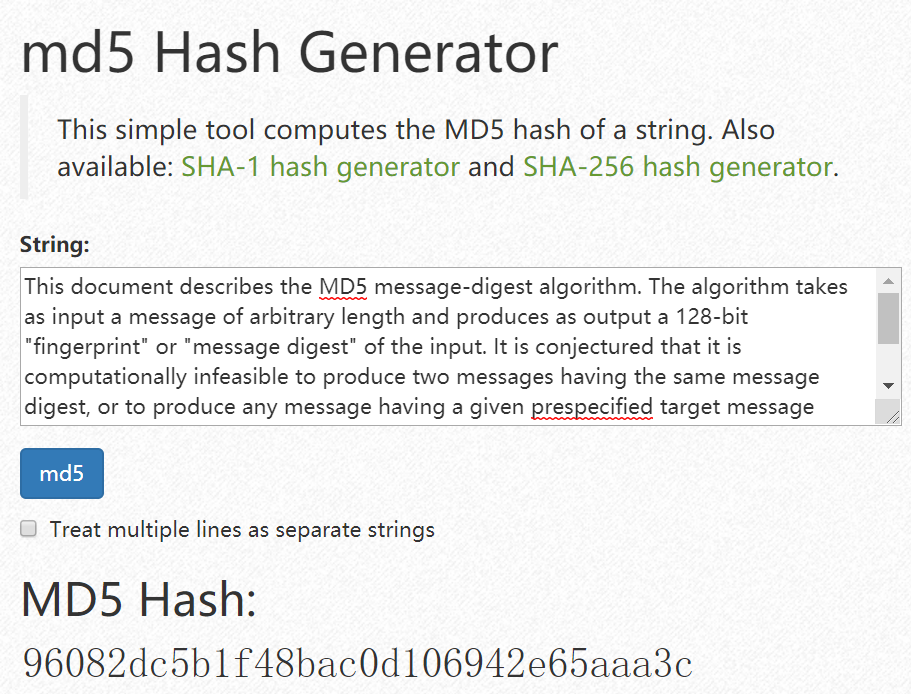
结果都是为96082dc5b1f48bac0d106942e65aaa3c

结果说明该 MD5 算法符合标准