🎨 CV | 使用 Golang 实现 JPEG 解码器

这里使用 Golang 来实现一个 JPEG 编码器，并且将其结果与 GIF 格式做一个比较

🚀 代码: Github

在实现 JPEG 解码器之前，这里顺便提一下自适应 Huffman 编码。

自适应 Huffman 编码

1543223378152

(a)

一般情况下，对于一段数据进行 Huffman 编码需要先得到完整的数据，根据数据中各个字符出现的概率来对每个字符进行编码，这样就要求 Huffman 编码之前必须要得到被编码数据的先验统计。根据这些统计数据，对出现频率较高的字符优先使用比较短的编码。在解码的时候，就需要编码后的数据以及编码表。这样问题就来了，对于一些不能获取先验统计的数据（如直播流的数据），一般 Huffman 编码就无法构造出较优的编码表，因此，就需要自适应 Huffman 编码

自适应 Huffman 编码的统计数据是根据数据流的到达而自动生成的，不依赖于数据的先验统计，而是基于目前为止实际收到的数据。

(b)

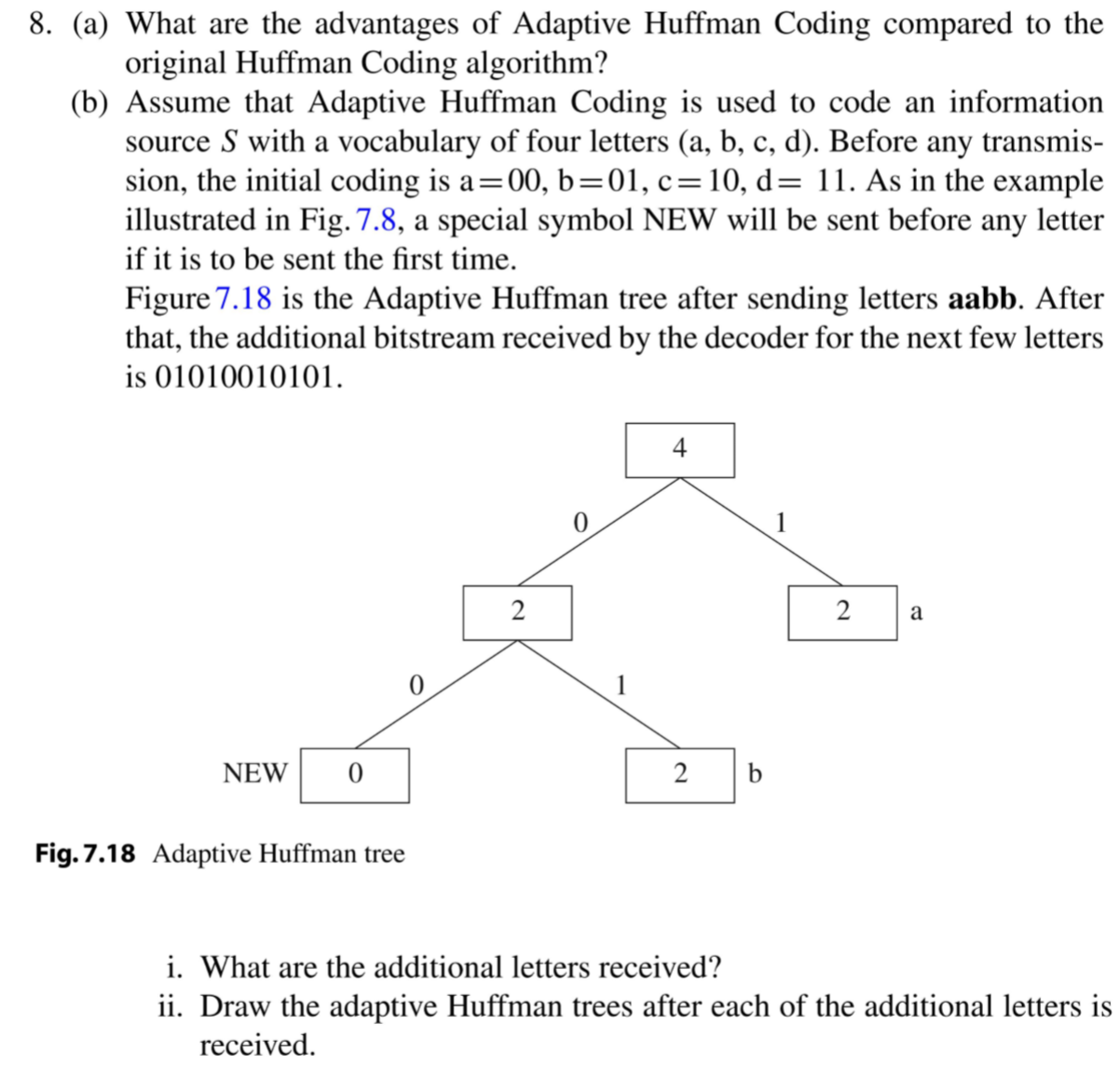
(i)

01010010101 解码成字符为：bacc

01 - b

01 - a

0010 - c

101 - c

具体的推导过程看下面。

(ii)

首先从收到的数据最开始解码，01在原来的 Huffman 树对应的字符为b，b在树中的计数加一，并且和具有计数 2 的最远的节点a进行交换，得到下面的新的哈夫曼树，然后更新父节点计数，直到根节点。

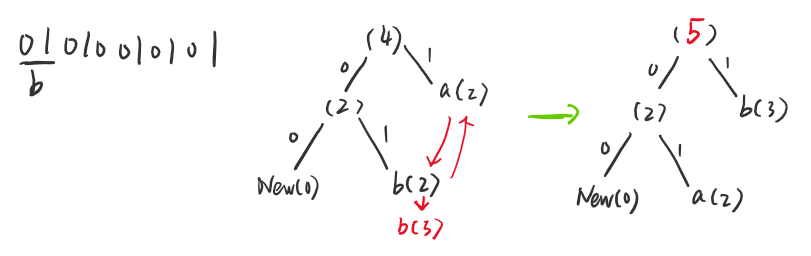
1543247529262

然后01在新的 Huffman 树对应的字符为a，再次更新树，由于不存在计数为 2 的节点，因此不需要交换，父节点也更新计数，也不存在需要交换的节点。

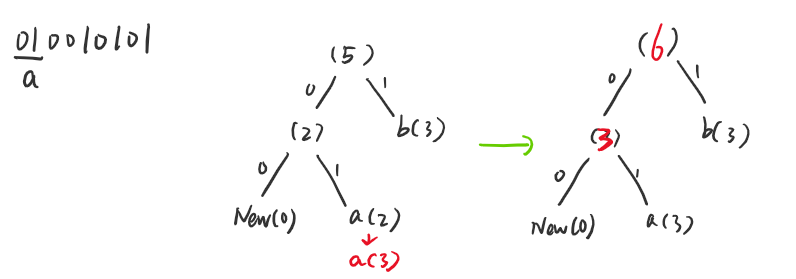
1543247593970

然后树中的00表示一个新的字符，是不存在树中的，因此需要在初始的编码表中找，后面的10对应的正是c，加入树中，然后更新父节点，更新到 4 的时候发现存在计数为 3 的节点，因此再次进行交换，生成下面的树，再次更新父节点的计数，直到根节点。

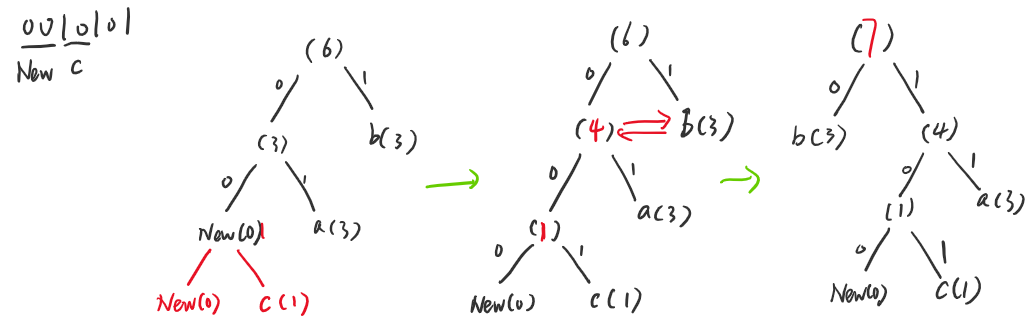
1543247628672

然后101在树中对应的字符为c，再次更新计数，不存在需要交换的节点

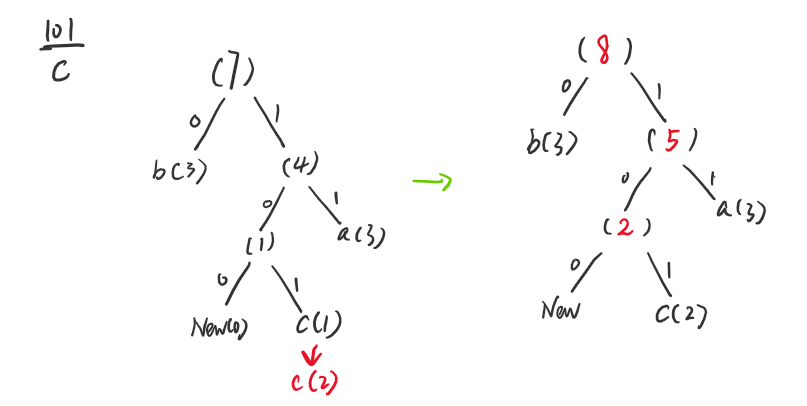
1543247709522

因此，最后解码出来的字符串为bacc

JPEG 编码器

1543223318879

分析

GIF 是一种采用 8 位色（256 种），使用 LZW 压缩算法对图片进行无损压缩的图片格式，十分适用于一些色彩简单的图片，对于一些计算机生成的卡通图片、线框图、LOGO 之类的图片可以达到比较理想的压缩率并且保持图片的质量。它采用全局色彩表（如果存在）构成一个 24 位 RGB 元组的调色板（每种底色为一个字节），来表示每个像素，不适用于真彩色的图片。

JPEG 是一种有损的压缩图片格式，把图片划分成若干个 8*8 的块进行有损压缩。对于一些色彩丰富，具有渐变色的图片可以在尽可能保持图片质量的情况下，去掉一些人眼很难察觉到的细节，达到比较好的压缩率。而对于一些内容变化缓慢的图片，JPEG 可以取得更好的压缩效果。

对于计算机生成的图片，如果色彩比较简单的话，使用 GIF 可以得到质量更好，体积更小的图片。但是如果卡通图片中颜色较多，并且存在大量的渐变色的话，GIF 会使得图片色彩严重损失，此时 JPEG 反而有更好的质量。

对于拍摄的照片，一般情况下色彩是比较复杂的，并且图片内容的过渡是缓慢的，使用 JPEG 可以在保持高质量的同时取得较高的压缩效果，如果使用 GIF 的话有可能导致色彩的损失。

程序实现

程序使用 GO 语言实现

代码仓库： Github

JPEG 编码器总体结构

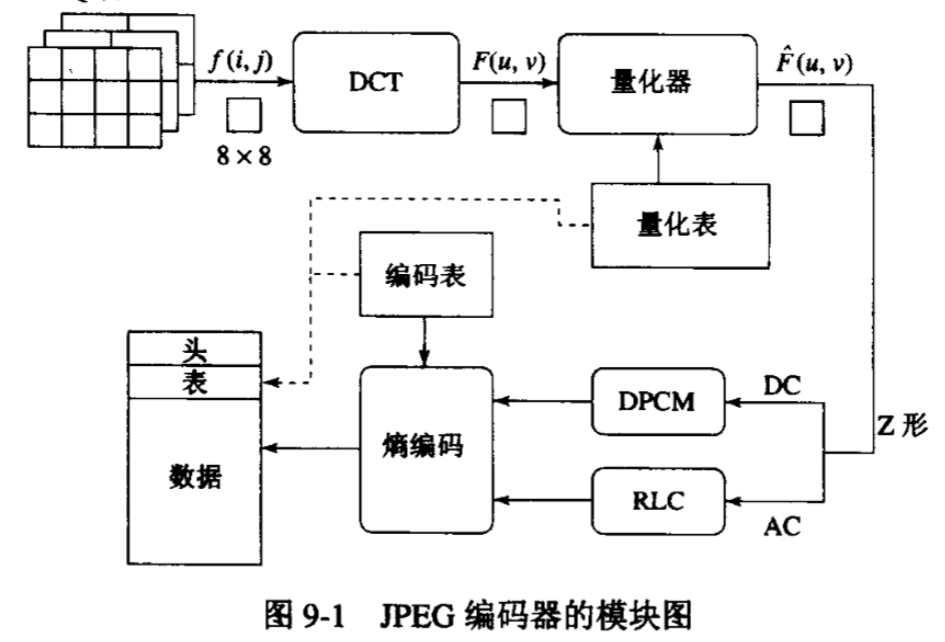
1543225347600

模块分解

按照 JPEG 编码的总体结构，将其划分为以下模块：

颜色转换：RGB to YUV
二次采样：4：2：0
离散余弦变换：2D DCT
量化器：Y 量化、UV 量化
无损压缩编码：
- DPCM 编码
- Z 形游长编码
熵编码： Huffman 编码

颜色转换和二次采样

由于人眼对于亮度远比色彩敏感，因此 JPEG 在压缩方面尽量保留亮度而在色彩部分做压缩。因此，需要先把亮度和色彩分离开来，这里使用 YUV 色彩模型。

首先，我们获取到图片各个像素点的 RGB，根据维基百科上的公式，将其转换为 YUV

1543225973412

根据 JPEG 的标准，对于上面得到的 YUV 进行色彩的二次采样，采用 4:2:0 的模式。尽量保留亮度信息而舍弃部分的颜色信息。它指的是对每行扫描线来说，只有一种色度分量以 2:1 的抽样率存储。相邻的扫描行存储不同的色度分量，也就是说，如果一行是 4:2:0 的话，下一行就是 4:0:2，再下一行是 4:2:0…以此类推。

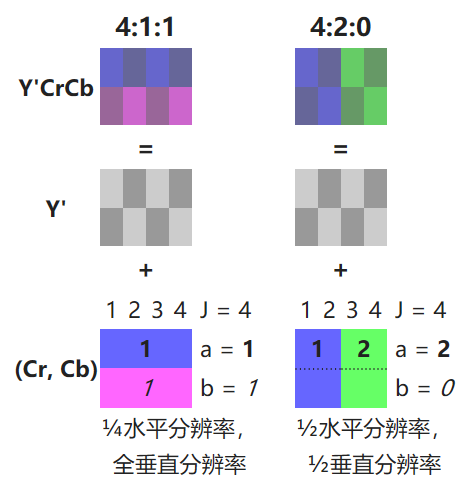
1543232658646

具体来说，就是映射成以下的模式

1 2	[Yo0 Uo0 Ve0] [Yo1 Uo0 Ve0] [Yo2 Uo2 Ve2] [Yo3 Uo2 Ve2] [Ye0 Uo0 Ve0] [Ye1 Uo0 Ve0] [Ye2 Uo2 Ve2] [Ye3 Uo2 Ve2]

另外，JPEG 对于图片是分成 8*8 的块处理的，对于不足 8 个像素的边缘，这里采取补 0 的方法进行填充

具体代码实现如下：

// RGB to YIQ and reSampling
func convertToYIQ(src image.Image) [][][3]int {
	bounds := src.Bounds().Max
	mat := make([][][3]int, bounds.Y+(8-bounds.Y%8))
	for x := 0; x < bounds.Y; x++ {
		row := make([][3]int, bounds.X+(8-bounds.X%8))
		for y := 0; y < bounds.X; y++ {
			r, g, b, _ := src.At(y, x).RGBA()
			R, G, B := float32(r/257), float32(g/257), float32(b/257)
			// RGB to YUV
			row[y][0] = int(uint8(0.299*R + 0.587*G + 0.114*B))
			// 4:2:0 二次采样
			if y%2 == 0 {
				row[y][1] = int(uint8(-0.1687*R - 0.3313*G + 0.5*B + 128))
				row[y][2] = int(uint8(0.5*R - 0.4187*G - 0.0813*B + 128))
				if x%2 == 1 {
					row[y][1] = int(row[y][1])
					row[y][2] = int(row[y][2])
					row[y+1][1] = row[y][1]
					row[y+1][2] = row[y][2]
					mat[x-1][y][1] = row[y][1]
					mat[x-1][y][2] = row[y][2]
					mat[x-1][y+1][1] = row[y][1]
					mat[x-1][y+1][2] = row[y][2]
				}
			}
		}
		mat[x] = row
	}
  // 补全
	for i := bounds.Y; i < len(mat); i++ {
		row := make([][3]int, bounds.X+(8-bounds.X%8))
		mat[i] = row
	}
	return mat
}

二维离散余弦变换

离散余弦变换是一种将分散的数据集中起来的变换技术。在 8*8 的矩阵当中，把信息尽可能集中在左上角，解除信息之间的相关性。以便对数据进行更好的压缩。

1543233164490

其中

1543233205606

我们对于每个 8*8 的块分别进行 DCT

代码实现如下：

// DCT离散余弦变换
func convertDCT(src [][][3]int, x, y int) [][][3]int {
	cSrc := make([][][3]int, 8)
	for k := 0; k < 8; k++ {
		cSrc[k] = make([][3]int, 8)
		copy(cSrc[k], src[x+k][y:y+8])
	}

	for k := 0; k < 3; k++ {
		for i := 0; i < 8; i++ {
			for j := 0; j < 8; j++ {
				cU, cV := 1.0, 1.0
				if i == 0 {
					cU = math.Sqrt(2) / 2.0
				}
				if j == 0 {
					cV = math.Sqrt(2) / 2.0
				}
				res := (cU * cV) / 4.0

				var value float64
				for a := 0; a < 8; a++ {
					for b := 0; b < 8; b++ {
						value += math.Cos(float64(2*a+1)*float64(i)*float64(math.Pi)/16.0) *
							math.Cos(float64(2*b+1)*float64(j)*float64(math.Pi)/16.0) *
							float64(cSrc[a][b][k])
					}
				}
				res = res * value
				src[x+i][y+j][k] = int(math.Round(res))
			}
		}
	}
	return src
}

量化

量化就是 JPEG 有损压缩的主要损失部分，通过对亮度 Y 和色彩 UV 采用不同的量化表，对色彩进行更大的压缩

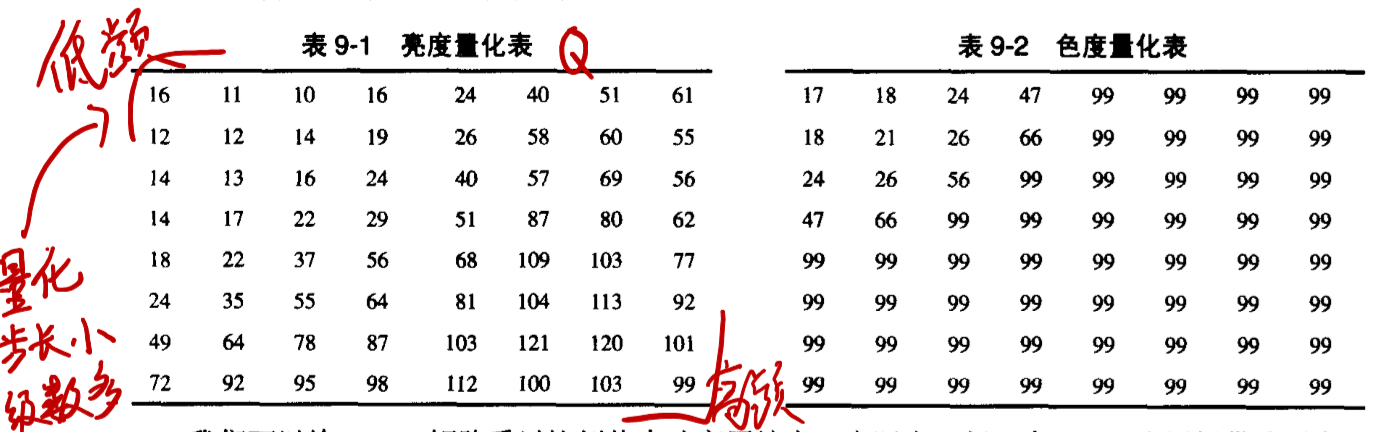
1543233573005

对于上面 DTC 之后得到的 8*8 的块进行量化

基本的操作公式如下：

1543233600660

代码实现如下：

// 量化
func quantitative(src [][][3]int, x, y int) [][][3]int {
	// Y
	for i := 0; i < 8; i++ {
		for j := 0; j < 8; j++ {
			src[x+i][y+j][0] =
      				int(math.Round(float64(src[x+i][y+j][0]) / float64(matrixY[i][j])))
		}
	}
	// UV
	for i := 0; i < 8; i++ {
		for j := 0; j < 8; j++ {
			src[x+i][y+j][1] =
      				int(math.Round(float64(src[x+i][y+j][1]) / float64(matrixIQ[i][j])))
			src[x+i][y+j][2] =
      				int(math.Round(float64(src[x+i][y+j][2]) / float64(matrixIQ[i][j])))
		}
	}
	return src
}

Z 形扫描和游长编码

经过量化之后，块数据当中就会存在大量的 0，而非零数据一般都集中在块的左上角，因此对其进行ZigZag编码

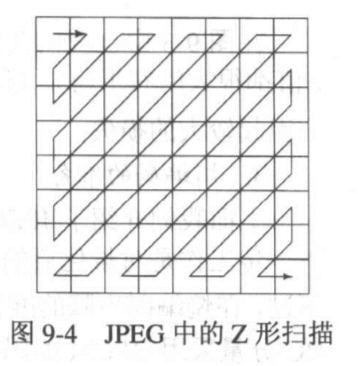
1543234333097

其代码实现如下：

func traverseZigZag(src [][][3]int, x, y int) ([][]factor, [3]int) {
	res := make([][]factor, 3)
	var dc [3]int
	for k := 0; k < 3; k ++ {
    // Z形扫描
		var zig []int
		i, j, up := 0, 0, 1
		turned := false
		d := [2][2]int{{1, -1}, {-1, 1}}
		corner := [2][4]int{{1, 0, 0, 1}, {0, 1, 1, 0}}
		for i < 8 && j < 8 {
			zig = append(zig, src[x+i][y+j][k])
			if i == 0 || j == 0 || i == 7 || j == 7 {
				if !turned {
					k := 2 * (up*(j/7) | (1-up)*(i/7))
					i += corner[up][k]
					j += corner[up][k+1]
					turned = true
					up = 1 - up
					continue
				} else {
					turned = false
				}
			}
			i += d[up][0]
			j += d[up][1]
		}
    // AC游长编码
    var dst []factor
		count := 0
		for i := 1; i < 64; i++ {
			if zig[i] != 0 {
				dst = append(dst, factor{count, zig[i]})
				count = 0
			} else {
				count++
				for count > 15 {
					dst = append(dst, factor{15, 0})
					count -= 15
				}
			}
		}
		dst = append(dst, factor{0, 0})
		res[k] = dst
    // DC
		dc[k] = zig[0]
	}
	return res, dc
}

然后，我们得到了一个按 Z 形扫描排序的数组zig

取其第一位作为这一块的 DC 系数，对于剩下的 AC 系数进行游长编码，用(RunLength, Value)，其中RunLength表示前面连续的 0 的个数，Value表示连续的 0 之后第一个非 0 的 AC 系数。并且以(0,0)作为结束标志。

为了方便后面的Huffman编码，这里的RunLength取 4 位，超过 4 位的就分割成多个(15,0)表示。

DPCM 编码

DC 系数虽然很大，但是相邻的块之间的 DC 系数编码却不大，因此对其进行DPCM编码

代码实现如下

// DPCM编码
func dcDPCM(mat [][3]int) [3][]int {
	var dst [3][]int
	for k := 0; k < 3; k++ {
		var row []int
		last := mat[0][k]
		for i := range mat {
			if i == 0 {
				row = append(row, last)
			} else {
				row = append(row, mat[i][k]-last)
				last = mat[i][k]
			}
		}
		dst[k] = row
	}
	return dst
}

Huffman 编码

首先，我们先来写一个 Huffman 树的生成函数

输入为各个值出现的次数，输出的为各个值对应的 Huffman 编码

首先将各个值以出现的次数作为权重，生成叶子节点数组

然后对于这些节点进行排序，每次从中取出权重最小的两个节点，合成一个节点之后再次按顺序放入数组。

直到数组剩下 1 个节点之后，这个节点就是 Huffman 树的根节点。

最后从这个根节点开始后序遍历，生成各个叶子节点对应的 Huffman 编码

代码如下：

type Node struct {
	Value  int
	Weight int
	Left   *Node
	Right  *Node
}

type Nodes []Node

func (n Nodes) Len() int {
	return len(n)
}

func (n Nodes) Less(i, j int) bool {
	return n[i].Weight < n[j].Weight
}

func (n Nodes) Swap(i, j int) {
	n[i], n[j] = n[j], n[i]
}

var Root *Node

func huffmanEncode(priorityMap map[int]int) map[int]string {
	nodes := makeSortedNodes(priorityMap)
	hfmRoot := makeHuffmanTree(nodes)
	return encodeTree(hfmRoot)
}
// 排序节点
func makeSortedNodes(priorityMap map[int]int) []Node {
	var nodeList Nodes
	for k, v := range priorityMap {
		nodeList = append(nodeList, Node{k, v, nil, nil})
	}
	sort.Sort(nodeList)
	return nodeList
}
// 构造Huffman树
func makeHuffmanTree(nodes Nodes) *Node {
	if len(nodes) < 2 {
		return &nodes[0]
	}
	for len(nodes) > 1 {
		a := nodes[0]
		b := nodes[1]
		father := Node{-1, a.Weight + b.Weight, &a, &b}
		oldLen := len(nodes)
		for i := 2; i < len(nodes); i++ {
			if father.Weight < nodes[i].Weight {
				nodes = append(nodes, Node{})
				for j := len(nodes) - 1; j > i ; j-- {
					nodes[j] = nodes[j - 1]
				}
				nodes[i] = father
				break
			}
		}
		if oldLen == len(nodes) {
			nodes = append(nodes, father)
		}
		nodes = nodes[2:]
	}
	return &nodes[0]
}
// 生成Huffman编码
func encodeTree(root *Node) map[int]string {
	var initialCode string
	encodeMap := make(map[int]string)
	root.traverse(initialCode, func(value int, code string) {
		encodeMap[value] = code
	})
	return encodeMap
}
// 后序遍历
func (n Node) traverse(code string, visit func(int, string)) {
	if left := n.Left; left != nil {
		left.traverse(code + "0", visit)
	} else {
		visit(n.Value, code)
		return
	}
	n.Right.traverse(code + "1", visit)
}

对于 DC 系数，我们以(Size, Amplitude)的格式存储，对于Size进行 Huffman 编码，而Amplitude的变化过大，因此直接存储。

具体代码如下：

func huffmanDC(dc [3][]int) []byte {
	table := make(map[int]int)
	var data []factor
  // 统计各个Size出现的频率
	for colorChannel := range dc {
		for _, d := range dc[colorChannel] {
			size := getLength(d)
			table[size]++
			data = append(data, factor{size, d})
		}
	}
  // 生成Huffman编码
	dcTable := huffmanEncode(table)
	bitData := bitArray{}
	for i := range data {
		dc := data[i]
		sizeStr := dcTable[dc.Length]
		sizeByte := []byte(sizeStr)
    // 写入Size的Huffman编码
		for _, b := range sizeByte {
			bitData.addBit(b - '0')
		}
    // 写入Amplitude数据
		bitData.addData(dc.Data)
	}
	return bitData.Data
}

对于 AC 系数，将(RunLength, Value)转换成Symbol1和Symbol2,

其中Symbol1为(Runlength, Size)，两者都是用 4 位来表示，由于上面游长编码已经处理过了，这就就可以直接整合成一个字节，对其进行 Huffman 编码

而Symbol2为(Amplitude)，直接存储。

func huffmanAC(ac [][][]factor) []byte {
	table := make(map[int]int)
	var data []factor
	// 统计各个Symbol1出现的频率
	for i := range ac {
		for colorChannel := range ac[i] {
			for _, d := range ac[i][colorChannel] {
				size := getLength(d.Data)
				symbol1 := d.Length*16 + size
				table[symbol1]++
				data = append(data, factor{symbol1, d.Data})
			}
		}
	}
	// 生成Huffman编码
	dcTable := huffmanEncode(table)
	bitData := bitArray{}
	for i := range data {
		ac := data[i]
		sizeStr := dcTable[ac.Length]
		sizeByte := []byte(sizeStr)
		// 写入 Symbol1 的Huffman编码
		for _, b := range sizeByte {
			bitData.addBit(b - '0')
		}
		// 写入Amplitude数据
		bitData.addData(ac.Data)
	}
	return bitData.Data
}

到此，我们完成了 JPEG 的各个模块。

JPEG 编码

首先是从文件中读取图片，读取其 RGB 颜色信息

func Make(src, dst string) {
	file1, err := os.OpenFile(src, os.O_RDONLY, 0)
	check(err)
	defer file1.Close()
	img, err := jpeg.Decode(file1)
	check(err)
	err = encode(img, dst)
	check(err)
}

以下是 JPEG 编码器的整个过程的具体实现

func encode(src image.Image, dst string) error {
	fmt.Println("Encode JPEG for ", dst)
	fmt.Println("RGB to YUV")
	// RGB to YUV 颜色模型转换
	imgColor := convertToYUV(src)
	fmt.Println("Size: ", len(imgColor), len(imgColor[0]))
	// AC[第i块数据][0:Y, 1:I, 2:Q][第i对AC系数]
	var AC [][][]factor
	// DC[第i块数据][0:Y, 1:I, 2:Q]
	var DC [][3]int
	fmt.Println("DCT...")
	fmt.Println("Quantitative...")
	fmt.Println("ZigZag...")
	// 每次对8*8大小的块操作
	for x := 0; x < len(imgColor); x += 8 {
		for y := 0; y < len(imgColor[x]); y += 8 {
			// 2D DCT
			convertDCT(imgColor, x, y)
			// 量化
			quantitative(imgColor, x, y)
			// Z扫描生成AC系数的游长编码和DC系数
			ac, dc := traverseZigZag(imgColor, x, y)
			AC = append(AC, ac)
			DC = append(DC, dc)
		}
	}
	// allDC[0:Y, 1:I, 2:Q][第i块数据]
	fmt.Println("DPCM...")
	// DC系数的DPCM编码
	allDC := dcDPCM(DC)
	fmt.Println("Huffman for DC...")
	// DC系数的Huffman编码
	DCBinary := huffmanDC(allDC)
	fmt.Println("Huffman for AC...")
	// AC系数的Huffman编码
	ACBinary := huffmanAC(AC)
	fmt.Println("Output Binary...")
	// 输出二进制数据
	var finalData []byte
	finalData = append(finalData, DCBinary...)
	finalData = append(finalData, ACBinary...)
	err = ioutil.WriteFile(dst+".binary", finalData, 0644)
	check(err)
}

JPEG 解码模块

由于需要对比 JPEG 编码后的图片和原图之间的差异，因此需要解码回原来的 RGB 并且写入文件。

由于后面的 Huffman 编码、AC 系数的 Z 形游长编码还有 DC 系数的 DPCM 都是属于无损压缩编码，因此解码部分就直接从量化之后开始进行。

要实现解码，就要先实现以下模块:

反量化
2D DCT 逆变换
YUV 转换 RGB

反量化

量化是将原来的值除量化表中的值来减少数据的位数，而反过来就需要数据乘回量化表中对应的值。

其基本结构和原来的差不多

// 反量化
func Iquantitative(src [][][3]int, x, y int) [][][3]int {
	// Y
	for i := 0; i < 8; i++ {
		for j := 0; j < 8; j++ {
			src[x+i][y+j][0] =
				int(math.Round(float64(src[x+i][y+j][0]) * float64(matrixY[i][j])))
		}
	}
	// UV
	for i := 0; i < 8; i++ {
		for j := 0; j < 8; j++ {
			src[x+i][y+j][1] =
				int(math.Round(float64(src[x+i][y+j][1]) * float64(matrixIQ[i][j])))
			src[x+i][y+j][2] =
				int(math.Round(float64(src[x+i][y+j][2]) * float64(matrixIQ[i][j])))
		}
	}
	return src
}

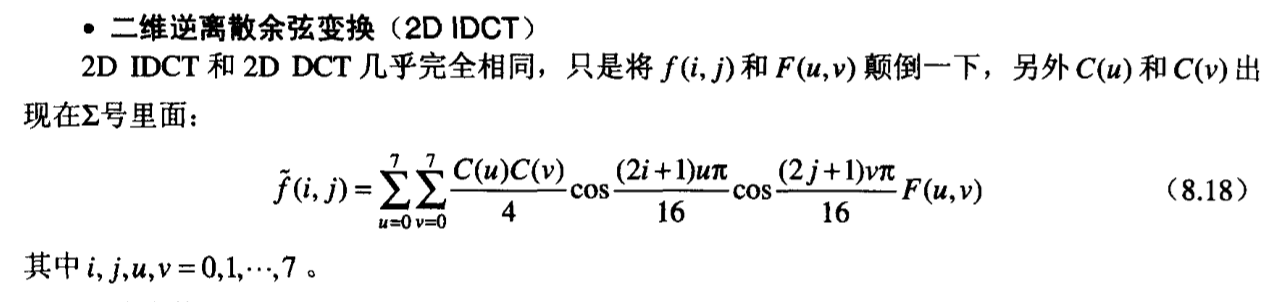
2D IDCT

逆 DCT 变化根据公式就可以实现，基本上和 DCT 是差不多的，只是将一部分放入了求和里面：

1543233239455

// IDTC逆离散余弦变换
func convertIDCT(src [][][3]int, x, y int) [][][3]int {
	cSrc := make([][][3]int, 8)
	for k := 0; k < 8; k++ {
		cSrc[k] = make([][3]int, 8)
		copy(cSrc[k], src[x+k][y:y+8])
	}
	for k := 0; k < 3; k++ {
		for i := 0; i < 8; i++ {
			for j := 0; j < 8; j++ {
				var res float64
				for u := 0; u < 8; u++ {
					for v := 0; v < 8; v++ {
						cU, cV := 1.0, 1.0
						if u == 0 {
							cU = math.Sqrt(2) / 2.0
						}
						if v == 0 {
							cV = math.Sqrt(2) / 2.0
						}
						value := (cU * cV) / 4.0
						value *= math.Cos(float64(2*i+1)*float64(u)*float64(math.Pi)/16.0) *
							math.Cos(float64(2*j+1)*float64(v)*float64(math.Pi)/16.0) *
							float64(cSrc[u][v][k])
						// fmt.Println(value)
						res += value
					}
				}
				// fmt.Println("res:", res)
				src[x+i][y+j][k] = int(math.Round(res))
			}
		}
	}
	return src
}

YUV 转换 RGB

YUV 转换成 RGB 也是根据之前的转换再进行一次逆转换就可以了

1543239535934

func convertRGB(mat [][][3]int) [][][3]int {
	weight := len(mat)
	height := len(mat[0])
	for x := 0; x < weight; x++ {
		for y := 0; y < height; y++ {
			Y, U, V := mat[x][y][0], mat[x][y][1],mat[x][y][2]
			mat[x][y][0] = Y + int(1.402 * float32(V- 128))
			mat[x][y][1] = Y - int(0.34414 * float32(U- 128)) - int(0.71414 * float32(V- 128))
			mat[x][y][2] = Y + int(1.772 * float32(U- 128))
			for i := 0; i < 3; i++ {
				if mat[x][y][i] < 0 {
					mat[x][y][i] = 0
				} else if mat[x][y][i] > 255 {
					mat[x][y][i] = 255
				}
			}
		}
	}
	return mat
}

JPEG 解码

具体实现代码如下：

// 解码
fmt.Println("Decode...")
fmt.Println("Inverse quantitative...")
fmt.Println("Inverse DTC...")
for x := 0; x < len(imgColor); x += 8 {
  for y := 0; y < len(imgColor[x]); y += 8 {
    // 反量化
    Iquantitative(imgColor, x, y)
    // 2D DCT 逆变换
    convertIDCT(imgColor, x, y)
  }
}
fmt.Println("YUV to RGB...")
// 转换成RGB
convertRGB(imgColor)

// 写入文件
fmt.Println("Write Image...")
bounds := src.Bounds().Max
dstImage := image.NewRGBA(src.Bounds())
for x := 0; x < bounds.Y; x++ {
  for y := 0; y < bounds.X; y++ {
    dstImage.Set(y, x, color.RGBA{
      R: uint8(imgColor[x][y][0]),
      G: uint8(imgColor[x][y][1]),
      B: uint8(imgColor[x][y][2]), A: 255 })
  }
}
distFile, err := os.Create(dst)
check(err)
fmt.Println("Write File...")
err = jpeg.Encode(distFile, dstImage, &jpeg.Options{Quality: 100})
check(err)

fmt.Println("Finish!")
return nil

GIF 编码

GIF 编码这里采取了现成的库

具体代码实现如下：

func Make(src, dst string) {
	// 打开原图
	file1, err := os.OpenFile(src, os.O_RDONLY, 0)
	check(err)
	defer file1.Close()
	// JPEG 解码
	img, err := jpeg.Decode(file1)
	check(err)
	distGif, err := os.Create(dst)
	check(err)
	// 生成 GIF
	outGif := &gif.GIF{}
	bounds := img.Bounds()
	// 生成 调色板
	palettedImage := image.NewPaletted(bounds, nil)
	// 中值取值算法计算256色
	quantizer := gogif.MedianCutQuantizer{NumColor: 256}
	// 量化
	quantizer.Quantize(palettedImage, bounds, img, image.ZP)
	// 加入GIF数据
	outGif.Image = append(outGif.Image, palettedImage)
	outGif.Delay = append(outGif.Delay, 0)
	// GIF 编码
	err = gif.EncodeAll(distGif, outGif)
	if err != nil {
		fmt.Println(err)
	}
}

结果分析

视觉效果比较

首先对比一下 JPEG 编码和 GIF 编码后的效果

卡通图

我们先来看看卡通图整体的效果

原图：

动物卡通图片

JPEG	GIF

从整体来看

JPEG 和原图对比基本上相同，人眼基本上看不错差别。

而 GIF 在天空部分则出现了明显的颜色分界，这应该是由于 GIF 只有 256 色而导致渐变色无法很好地还原。

这方面，JPEG 胜

再来看看细节部分

原图	JPEG	GIF

可以看到 GIF 在鳄鱼的身体部分的颜色损失十分严重，几乎只有一种颜色，则应该是由于这张图片颜色过多，256 种无法容纳这么多的颜色，而 JPEG 则不太明显。

JPEG 还原度更高

原图	JPEG	GIF

从大象的鼻子来看，可以发现 JPEG 编码之后的图片和原来的图片相比多出了很多噪点，这些噪点大多分布在各种线条和颜色之间的边缘的，而 GIF 更多是由于颜色损失而带来的噪点，使得各个部分的分界变得不太明显了，实际上的效果是比 JPEG 稍好的。

因此，这一部分，GIF 略胜一筹

再来看看放大后的细节

原图	JPEG	GIF

可以看出，JPEG 编码后的图片边缘有着明显的噪点，有着不应该出现的波动。原图的背景是有一个渐变效果的，而 GIF 的背景色几乎没有变化，不过他的噪点和扰动比 JPEG 要少。

细节部分，GIF 胜

再来看看照片之间的对比

原图：

动物照片

先来看看整体的效果

JPEG	GIF

一眼看去，这两者几乎没有区别，仔细看看牛后面的山坡，发现 GIF 和原图对比还是有一定的颜色差异的。

JPEG 效果更好

看看细节部分

原图	JPEG	GIF

对于原图，JPEG 和 GIF 都多出了不少噪点，应该都是由于压缩而损失的。而牛头上的阴影部分，GIF 颜色的差异就比较大，几乎糊成一片，JPEG 也有少少的损失。

JPEG 还原度更高

通过对比两张图两种格式和原图。可以发现在绝大多数情况下 JPEG 的视觉效果比 GIF 更好，这应该是由于这两张图片的颜色都远大于 256 色，通过 GIF 编码之后颜色会大量损失，造成了糟糕的视觉效果。在卡通图的细节上 GIF 有着一点优势。

压缩率对比

要比较压缩率，就需要先将原图转换成没有压缩的格式，比如 BMP

下面是生成的图片的大小

卡通图：

格式	大小	压缩率
BMP	2095KB	100%
JPEG	138KB	93.41%
GIF	252KB	87.97%

摄影图：

格式	大小	压缩率
BMP	2047KB	100%
JPEG	200KB	90.23%
GIF	498KB	75.67%

可以看出，在当前的编码参数情况下，JPEG的压缩率明显比 GIF 高10%左右

失真度对比

图片失真度可以通过计算像素的均方差来量度

// 均方差计算
sum := 0.0
count := 0
for x := 0; x < bounds.Max.X; x++ {
  for y := 0; y < bounds.Max.Y; y++ {
    for k := 0; k < 3; k ++ {
      sum += math.Pow(float64(rgbSrc[x][y][k] - rgbDst[x][y][k]), 2.0)
      count++
    }
  }
}

在代码中分别计算两张图的 GIF 和 JPEG 的均方差

卡通图

格式	均方差(MSE)
JPEG	49.22353006993007
GIF	60.063944988344986

摄像图

格式	均方差(MSE)
JPEG	34.2789236238392
GIF	50.549321656586024

上面的失真度数据可以看出，JPEG的失真度明显比 GIF 要低，也就是所还原效果更好。

而且对于摄像图 JPEG 有着极其明显的优势，这也是得益于 JPEG 对于内容变化缓慢的图片的压缩效果好的特性。

总结

对于这两张图片，JPEG 在总体视觉效果、压缩效果都明显优于 GIF，而 GIF 在部分细节上略有优势。

虽然说 GIF 对于计算机生成的颜色简单的图片很有优势，但是这里的卡通图的颜色明显远多于 256 种，而且处处存在着渐变和过渡，GIF 对于这种图就显得有点无力。

因此总体上看，在卡通图中 GIF 的颜色差异有点大，而在细节方面，GIF 略胜 JPEG 一筹，图片的噪点比较少。

而实际的摄像图来说，JPEG 在压缩原理上明显就比 GIF 更加有优势，而实际也是有着比较好的视觉效果和压缩效果。